| << Chapter < Page | Chapter >> Page > |
In many areas of pure and applied mathematics, we are interested in finding solutions to an equation of the form For most functions, however, it is difficult—if not impossible—to calculate their zeroes explicitly. In this section, we take a look at a technique that provides a very efficient way of approximating the zeroes of functions . This technique makes use of tangent line approximations and is behind the method used often by calculators and computers to find zeroes.
Consider the task of finding the solutions of If is the first-degree polynomial then the solution of is given by the formula If is the second-degree polynomial the solutions of can be found by using the quadratic formula. However, for polynomials of degree or more, finding roots of becomes more complicated. Although formulas exist for third- and fourth-degree polynomials, they are quite complicated. Also, if is a polynomial of degree or greater, it is known that no such formulas exist. For example, consider the function
No formula exists that allows us to find the solutions of Similar difficulties exist for nonpolynomial functions. For example, consider the task of finding solutions of No simple formula exists for the solutions of this equation. In cases such as these, we can use Newton’s method to approximate the roots.
Newton’s method makes use of the following idea to approximate the solutions of By sketching a graph of we can estimate a root of Let’s call this estimate We then draw the tangent line to at If this tangent line intersects the -axis at some point Now let be the next approximation to the actual root. Typically, is closer than to an actual root. Next we draw the tangent line to at If this tangent line also intersects the -axis, producing another approximation, We continue in this way, deriving a list of approximations: Typically, the numbers quickly approach an actual root as shown in the following figure.
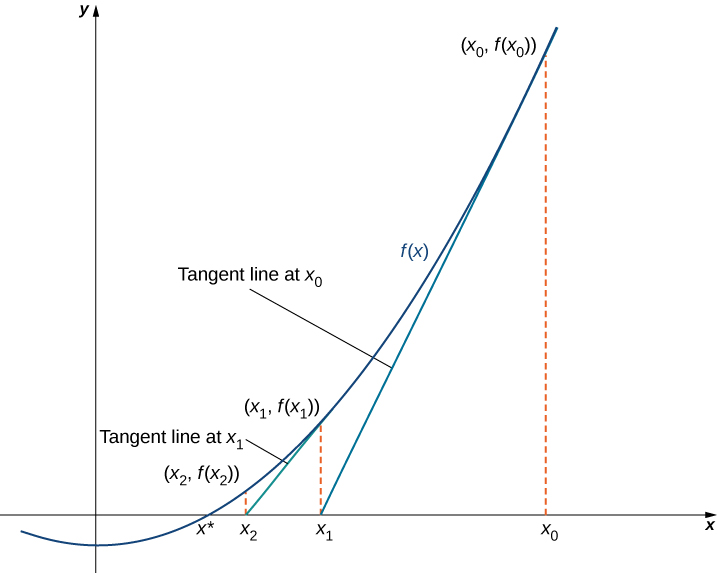
Now let’s look at how to calculate the approximations If is our first approximation, the approximation is defined by letting be the -intercept of the tangent line to at The equation of this tangent line is given by
Therefore, must satisfy
Solving this equation for we conclude that
Similarly, the point is the -intercept of the tangent line to at Therefore, satisfies the equation
In general, for satisfies
Next we see how to make use of this technique to approximate the root of the polynomial

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?