| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
Earlier in this chapter, we developed the properties of exponents for multiplication. We summarize these properties below.
If are real numbers, and are whole numbers, then
Now we will look at the exponent properties for division. A quick memory refresher may help before we get started. You have learned to simplify fractions by dividing out common factors from the numerator and denominator using the Equivalent Fractions Property. This property will also help you work with algebraic fractions—which are also quotients.
If are whole numbers where ,
As before, we’ll try to discover a property by looking at some examples.
Notice, in each case the bases were the same and we subtracted exponents.
When the larger exponent was in the numerator, we were left with factors in the numerator.
When the larger exponent was in the denominator, we were left with factors in the denominator—notice the numerator of 1.
We write:
This leads to the Quotient Property for Exponents .
If is a real number, , and are whole numbers, then
A couple of examples with numbers may help to verify this property.
Simplify: ⓐ ⓑ
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
| Since 9>7, there are more factors of x in the numerator. |
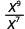 |
| Use the Quotient Property, . |
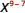 |
| Simplify. |
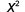 |
| Since 10>2, there are more factors of x in the numerator. |
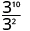 |
| Use the Quotient Property, . |
 |
| Simplify. |
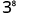 |
Simplify: ⓐ ⓑ
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
| Since 12>8, there are more factors of b in the denominator. |
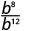 |
| Use the Quotient Property, . |
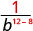 |
| Simplify. |
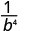 |
| Since 5>3, there are more factors of 3 in the denominator. |
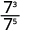 |
| Use the Quotient Property, . |
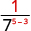 |
| Simplify. |
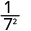 |
| Simplify. |
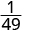 |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?