| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.
In this section, we will solve systems of linear equations by the substitution method.
We will use the same system we used first for graphing.
We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.
Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!
After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.
We’ll fill in all these steps now in [link] .
If one of the equations in the system is given in slope–intercept form, Step 1 is already done! We’ll see this in [link] .
Solve the system by substitution.
The second equation is already solved for
y . We will substitute the expression in place of
y in the first equation.
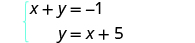 | |
| The second equation is already solved for
y .
We will substitute into the first equation. |
|
| Replace the y with x + 5. |
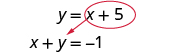 |
| Solve the resulting equation for x . |
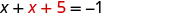 |
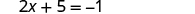 | |
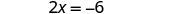 | |
| Substitute x = −3 into y = x + 5 to find y . |
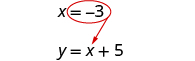 |
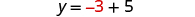 | |
| The ordered pair is (−3, 2). |
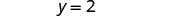 |
| Check the ordered pair in both equations:
|
|
| The solution is (−3, 2). |
If the equations are given in standard form, we’ll need to start by solving for one of the variables. In this next example, we’ll solve the first equation for y .

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?