| << Chapter < Page | Chapter >> Page > |
For each of the following exercises, solve the equation for y in terms of x .
For each of the following exercises, find the distance between the two points. Simplify your answers, and write the exact answer in simplest radical form for irrational answers.
Find the distance between the two points given using your calculator, and round your answer to the nearest hundredth.
and
For each of the following exercises, find the coordinates of the midpoint of the line segment that joins the two given points.
For each of the following exercises, identify the information requested.
If a point is located on the y -axis, what is the x -coordinate?
If a point is located on the x -axis, what is the y -coordinate?
For each of the following exercises, plot the three points on the given coordinate plane. State whether the three points you plotted appear to be collinear (on the same line).
Name the quadrant in which the following points would be located. If the point is on an axis, name the axis.
For each of the following exercises, construct a table and graph the equation by plotting at least three points.
For each of the following exercises, find and plot the x- and y -intercepts, and graph the straight line based on those two points.
For each of the following exercises, use the graph in the figure below.
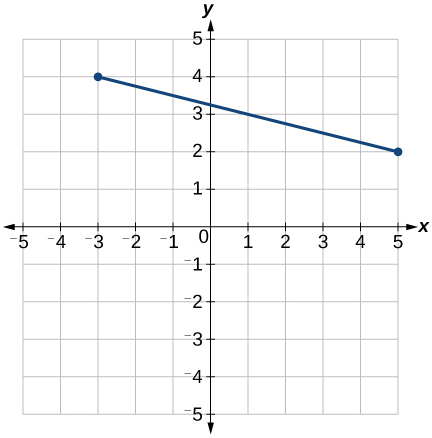
Find the distance between the two endpoints using the distance formula. Round to three decimal places.
Find the coordinates of the midpoint of the line segment connecting the two points.
Find the distance that is from the origin. Round to three decimal places.
For the following exercises, use your graphing calculator to input the linear graphs in the Y= graph menu.
After graphing it, use the 2 nd CALC button and 1:value button, hit enter. At the lower part of the screen you will see “x=” and a blinking cursor. You may enter any number for x and it will display the y value for any x value you input. Use this and plug in x = 0, thus finding the y -intercept, for each of the following graphs.
For the following exercises, use your graphing calculator to input the linear graphs in the Y= graph menu.
After graphing it, use the 2 nd CALC button and 2:zero button, hit enter. At the lower part of the screen you will see “left bound?” and a blinking cursor on the graph of the line. Move this cursor to the left of the x -intercept, hit ENTER. Now it says “right bound?” Move the cursor to the right of the x -intercept, hit enter. Now it says “guess?” Move your cursor to the left somewhere in between the left and right bound near the x -intercept. Hit enter. At the bottom of your screen it will display the coordinates of the x- intercept or the “zero” to the y -value. Use this to find the x -intercept.
Note: With linear/straight line functions the zero is not really a “guess,” but it is necessary to enter a “guess” so it will search and find the exact x -intercept between your right and left boundaries. With other types of functions (more than one x -intercept), they may be irrational numbers so “guess” is more appropriate to give it the correct limits to find a very close approximation between the left and right boundaries.
A man drove 10 mi directly east from his home, made a left turn at an intersection, and then traveled 5 mi north to his place of work. If a road was made directly from his home to his place of work, what would its distance be to the nearest tenth of a mile?
If the road was made in the previous exercise, how much shorter would the man’s one-way trip be every day?
mi shorter
Given these four points: find the coordinates of the midpoint of line segments and
After finding the two midpoints in the previous exercise, find the distance between the two midpoints to the nearest thousandth.
Given the graph of the rectangle shown and the coordinates of its vertices, prove that the diagonals of the rectangle are of equal length.
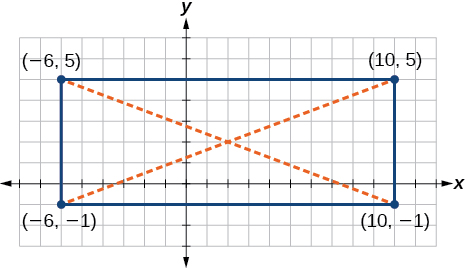
In the previous exercise, find the coordinates of the midpoint for each diagonal.
Midpoint of each diagonal is the same point Note this is a characteristic of rectangles, but not other quadrilaterals.
The coordinates on a map for San Francisco are and those for Sacramento are Note that coordinates represent miles. Find the distance between the cities to the nearest mile.
If San Jose’s coordinates are where the coordinates represent miles, find the distance between San Jose and San Francisco to the nearest mile.
mi
A small craft in Lake Ontario sends out a distress signal. The coordinates of the boat in trouble were One rescue boat is at the coordinates and a second Coast Guard craft is at coordinates Assuming both rescue craft travel at the same rate, which one would get to the distressed boat the fastest?
A man on the top of a building wants to have a guy wire extend to a point on the ground 20 ft from the building. To the nearest foot, how long will the wire have to be if the building is 50 ft tall?
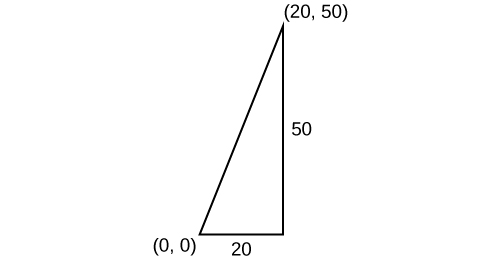
54 ft
If we rent a truck and pay a $75/day fee plus $.20 for every mile we travel, write a linear equation that would express the total cost using to represent the number of miles we travel. Graph this function on your graphing calculator and find the total cost for one day if we travel 70 mi.

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?