| << Chapter < Page | Chapter >> Page > |
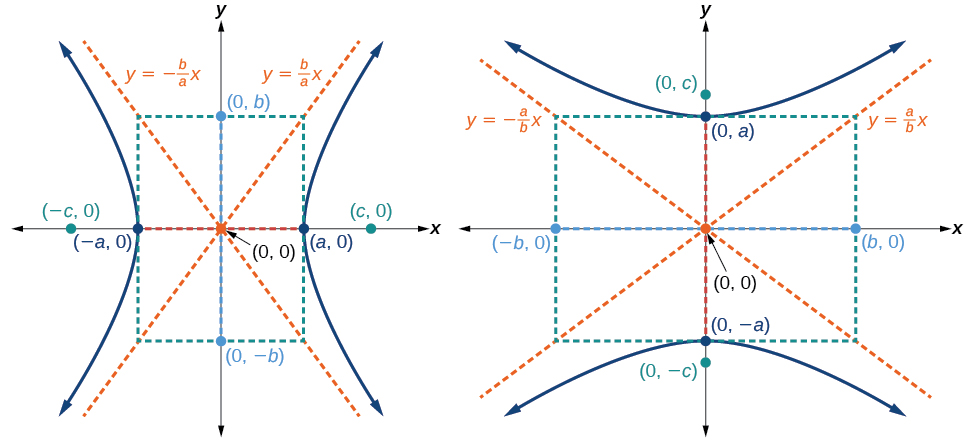
Given the equation of a hyperbola in standard form, locate its vertices and foci.
Identify the vertices and foci of the hyperbola with equation
The equation has the form so the transverse axis lies on the y -axis. The hyperbola is centered at the origin, so the vertices serve as the y -intercepts of the graph. To find the vertices, set and solve for
The foci are located at Solving for
Therefore, the vertices are located at and the foci are located at
Identify the vertices and foci of the hyperbola with equation
Vertices: Foci:
Just as with ellipses, writing the equation for a hyperbola in standard form allows us to calculate the key features: its center, vertices, co-vertices, foci, asymptotes, and the lengths and positions of the transverse and conjugate axes. Conversely, an equation for a hyperbola can be found given its key features. We begin by finding standard equations for hyperbolas centered at the origin. Then we will turn our attention to finding standard equations for hyperbolas centered at some point other than the origin.
Reviewing the standard forms given for hyperbolas centered at we see that the vertices, co-vertices, and foci are related by the equation Note that this equation can also be rewritten as This relationship is used to write the equation for a hyperbola when given the coordinates of its foci and vertices.
Given the vertices and foci of a hyperbola centered at write its equation in standard form.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?