| << Chapter < Page | Chapter >> Page > |
Now that we can find rational zeros for a polynomial function, we will look at a theorem that discusses the number of complex zeros of a polynomial function. The Fundamental Theorem of Algebra tells us that every polynomial function has at least one complex zero. This theorem forms the foundation for solving polynomial equations.
Suppose is a polynomial function of degree four, and The Fundamental Theorem of Algebra states that there is at least one complex solution, call it By the Factor Theorem, we can write as a product of and a polynomial quotient. Since is linear, the polynomial quotient will be of degree three. Now we apply the Fundamental Theorem of Algebra to the third-degree polynomial quotient. It will have at least one complex zero, call it So we can write the polynomial quotient as a product of and a new polynomial quotient of degree two. Continue to apply the Fundamental Theorem of Algebra until all of the zeros are found. There will be four of them and each one will yield a factor of
The Fundamental Theorem of Algebra states that, if is a polynomial of degree n>0 , then has at least one complex zero.
We can use this theorem to argue that, if is a polynomial of degree and is a non-zero real number, then has exactly linear factors
where are complex numbers. Therefore, has roots if we allow for multiplicities.
Does every polynomial have at least one imaginary zero?
No. Real numbers are a subset of complex numbers, but not the other way around. A complex number is not necessarily imaginary. Real numbers are also complex numbers.
Find the zeros of
The Rational Zero Theorem tells us that if is a zero of then is a factor of 3 and is a factor of 3.
The factors of 3 are and The possible values for and therefore the possible rational zeros for the function, are We will use synthetic division to evaluate each possible zero until we find one that gives a remainder of 0. Let’s begin with –3.
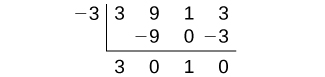
Dividing by gives a remainder of 0, so –3 is a zero of the function. The polynomial can be written as
We can then set the quadratic equal to 0 and solve to find the other zeros of the function.
The zeros of are –3 and
A vital implication of the Fundamental Theorem of Algebra , as we stated above, is that a polynomial function of degree will have zeros in the set of complex numbers, if we allow for multiplicities. This means that we can factor the polynomial function into factors. The Linear Factorization Theorem tells us that a polynomial function will have the same number of factors as its degree, and that each factor will be in the form where is a complex number.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?