| << Chapter < Page | Chapter >> Page > |
The first four terms are
Given the first term and the common factor, find the first four terms of a geometric sequence.
List the first four terms of the geometric sequence with and
Multiply by to find Repeat the process, using to find and so on.
The first four terms are
List the first five terms of the geometric sequence with and
A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is 9. Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.
The recursive formula for a geometric sequence with common ratio and first term is
Given the first several terms of a geometric sequence, write its recursive formula.
Write a recursive formula for the following geometric sequence.
The first term is given as 6. The common ratio can be found by dividing the second term by the first term.
Substitute the common ratio into the recursive formula for geometric sequences and define
Do we have to divide the second term by the first term to find the common ratio?
No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.
Write a recursive formula for the following geometric sequence.
Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.
Let’s take a look at the sequence This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2. An explicit formula for this sequence is
The graph of the sequence is shown in [link] .
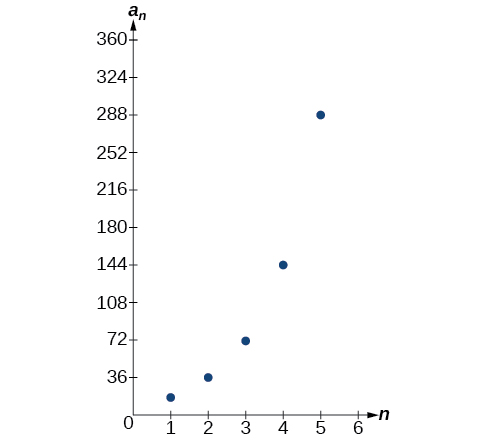
The n th term of a geometric sequence is given by the explicit formula :
Given a geometric sequence with and find
The sequence can be written in terms of the initial term and the common ratio
Find the common ratio using the given fourth term.
Find the second term by multiplying the first term by the common ratio.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?