| << Chapter < Page | Chapter >> Page > |
For the following exercises, use the explicit formula to write the first five terms of the arithmetic sequence.
For the following exercises, write an explicit formula for each arithmetic sequence.
For the following exercises, find the number of terms in the given finite arithmetic sequence.
For the following exercises, determine whether the graph shown represents an arithmetic sequence.
For the following exercises, use the information provided to graph the first 5 terms of the arithmetic sequence.
For the following exercises, follow the steps to work with the arithmetic sequence using a graphing calculator:
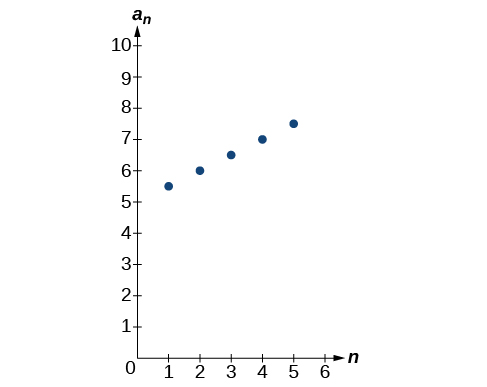
What are the first seven terms shown in the column with the heading
Use the scroll-down arrow to scroll to What value is given for
Press [WINDOW] . Set and Then press [GRAPH] . Graph the sequence as it appears on the graphing calculator.
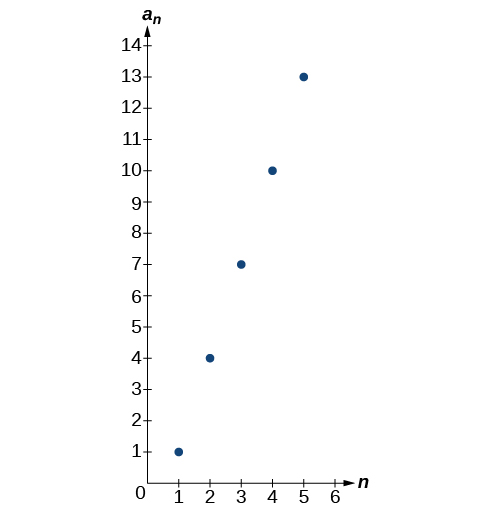
For the following exercises, follow the steps given above to work with the arithmetic sequence using a graphing calculator.
What are the first seven terms shown in the column with the heading in the TABLE feature?
Graph the sequence as it appears on the graphing calculator. Be sure to adjust the WINDOW settings as needed.
Give two examples of arithmetic sequences whose 4 th terms are
Give two examples of arithmetic sequences whose 10 th terms are
Answers will vary. Examples: and
Find the 5 th term of the arithmetic sequence
At which term does the sequence exceed 151?
At which term does the sequence begin to have negative values?
The sequence begins to have negative values at the 13 th term,
For which terms does the finite arithmetic sequence have integer values?
Write an arithmetic sequence using a recursive formula. Show the first 4 terms, and then find the 31 st term.
Answers will vary. Check to see that the sequence is arithmetic. Example: Recursive formula: First 4 terms:
Write an arithmetic sequence using an explicit formula. Show the first 4 terms, and then find the 28 th term.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?