| << Chapter < Page | Chapter >> Page > |
Halley’s Comet ( [link] ) orbits the sun about once every 75 years. Its path can be considered to be a very elongated ellipse. Other comets follow similar paths in space. These orbital paths can be studied using systems of equations. These systems, however, are different from the ones we considered in the previous section because the equations are not linear.

In this section, we will consider the intersection of a parabola and a line, a circle and a line, and a circle and an ellipse. The methods for solving systems of nonlinear equations are similar to those for linear equations.
A system of nonlinear equations is a system of two or more equations in two or more variables containing at least one equation that is not linear. Recall that a linear equation can take the form Any equation that cannot be written in this form in nonlinear. The substitution method we used for linear systems is the same method we will use for nonlinear systems. We solve one equation for one variable and then substitute the result into the second equation to solve for another variable, and so on. There is, however, a variation in the possible outcomes.
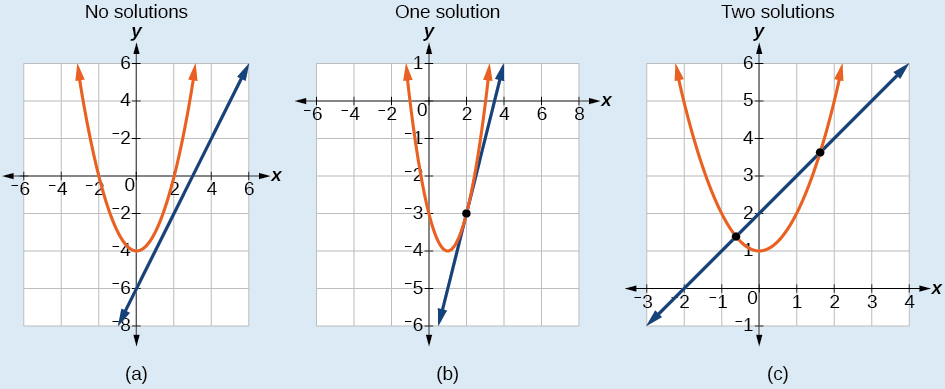
There are three possible types of solutions for a system of nonlinear equations involving a parabola and a line.
[link] illustrates possible solution sets for a system of equations involving a parabola and a line.
Given a system of equations containing a line and a parabola, find the solution.
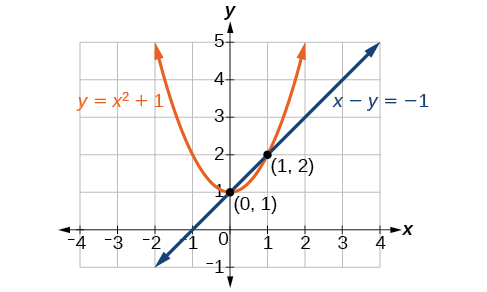
Solve the system of equations.
Solve the first equation for and then substitute the resulting expression into the second equation.
Expand the equation and set it equal to zero.
Solving for gives and Next, substitute each value for into the first equation to solve for Always substitute the value into the linear equation to check for extraneous solutions.
The solutions are and which can be verified by substituting these values into both of the original equations. See [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?