| << Chapter < Page | Chapter >> Page > |
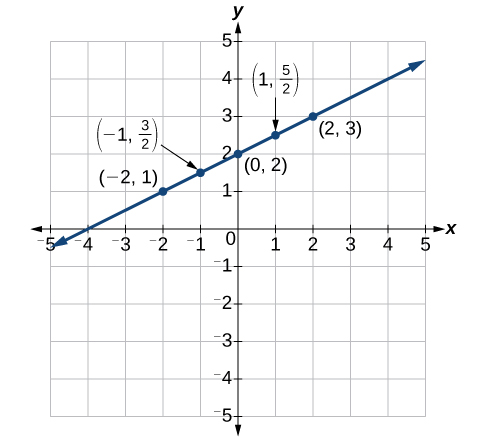
Construct a table and graph the equation by plotting points:
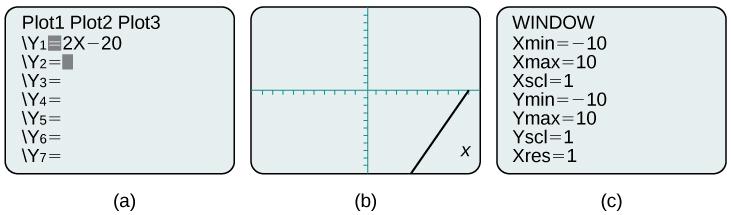
Most graphing calculators require similar techniques to graph an equation. The equations sometimes have to be manipulated so they are written in the style The TI-84 Plus, and many other calculator makes and models, have a mode function, which allows the window (the screen for viewing the graph) to be altered so the pertinent parts of a graph can be seen.
For example, the equation has been entered in the TI-84 Plus shown in [link] a. In [link] b, the resulting graph is shown. Notice that we cannot see on the screen where the graph crosses the axes. The standard window screen on the TI-84 Plus shows and See [link] c .
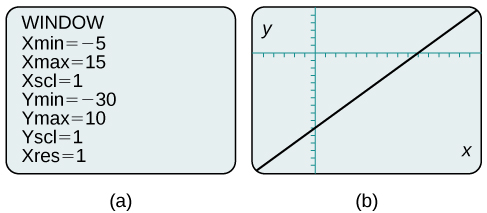
By changing the window to show more of the positive x- axis and more of the negative y- axis, we have a much better view of the graph and the x- and y- intercepts. See [link] a and [link] b.
Use a graphing utility to graph the equation:
Enter the equation in the y= function of the calculator. Set the window settings so that both the x- and y- intercepts are showing in the window. See [link] .
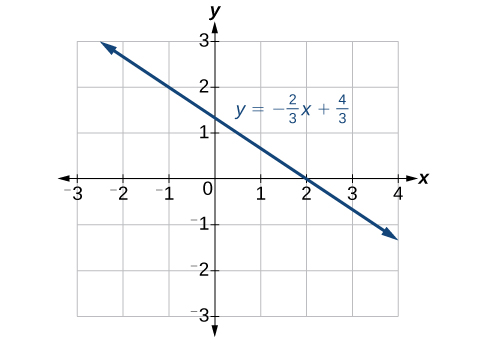
The intercepts of a graph are points at which the graph crosses the axes. The x- intercept is the point at which the graph crosses the x- axis. At this point, the y- coordinate is zero. The y- intercept is the point at which the graph crosses the y- axis. At this point, the x- coordinate is zero.
To determine the x- intercept, we set y equal to zero and solve for x . Similarly, to determine the y- intercept, we set x equal to zero and solve for y . For example, lets find the intercepts of the equation
To find the x- intercept, set
To find the y- intercept, set
We can confirm that our results make sense by observing a graph of the equation as in [link] . Notice that the graph crosses the axes where we predicted it would.
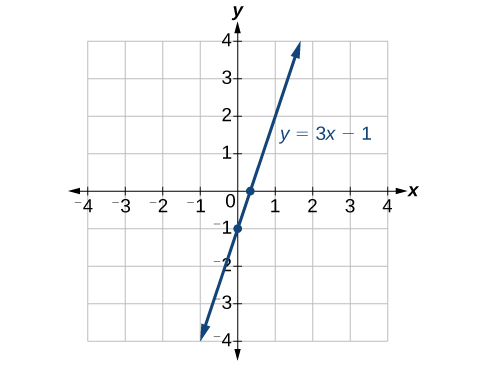
Find the intercepts of the equation Then sketch the graph using only the intercepts.
Set to find the x- intercept.
Set to find the y- intercept.
Plot both points, and draw a line passing through them as in [link] .
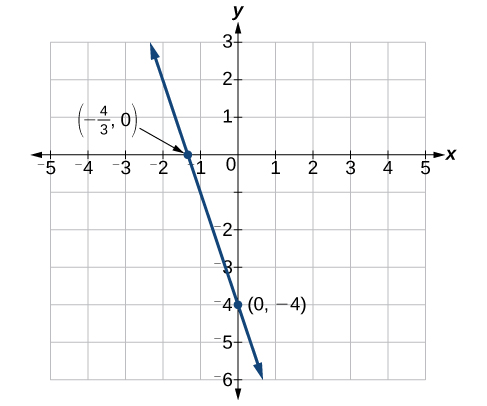
Find the intercepts of the equation and sketch the graph:
x -intercept is y- intercept is
Derived from the Pythagorean Theorem , the distance formula is used to find the distance between two points in the plane. The Pythagorean Theorem, is based on a right triangle where a and b are the lengths of the legs adjacent to the right angle, and c is the length of the hypotenuse. See [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?