| << Chapter < Page | Chapter >> Page > |
For the following exercises, find the equations of the asymptotes for each hyperbola.
For the following exercises, sketch a graph of the hyperbola, labeling vertices and foci.
For the following exercises, given information about the graph of the hyperbola, find its equation.
Vertices at and and one focus at
Center: vertex: one focus:
Center: vertex: one focus:
For the following exercises, given the graph of the hyperbola, find its equation.
For the following exercises, express the equation for the hyperbola as two functions, with as a function of Express as simply as possible. Use a graphing calculator to sketch the graph of the two functions on the same axes.
For the following exercises, a hedge is to be constructed in the shape of a hyperbola near a fountain at the center of the yard. Find the equation of the hyperbola and sketch the graph.
The hedge will follow the asymptotes and its closest distance to the center fountain is 5 yards.
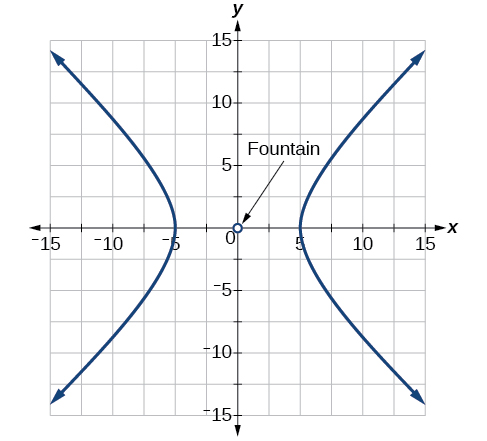
The hedge will follow the asymptotes and its closest distance to the center fountain is 6 yards.
The hedge will follow the asymptotes and and its closest distance to the center fountain is 10 yards.
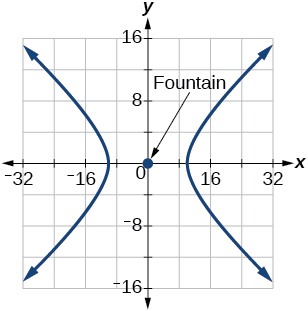
The hedge will follow the asymptotes and and its closest distance to the center fountain is 12 yards.
The hedge will follow the asymptotes and its closest distance to the center fountain is 20 yards.
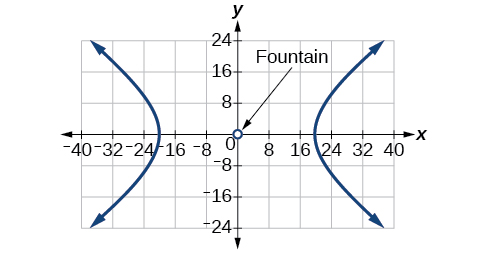
For the following exercises, assume an object enters our solar system and we want to graph its path on a coordinate system with the sun at the origin and the x-axis as the axis of symmetry for the object's path. Give the equation of the flight path of each object using the given information.
The object enters along a path approximated by the line and passes within 1 au (astronomical unit) of the sun at its closest approach, so that the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line
The object enters along a path approximated by the line and passes within 0.5 au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line
The object enters along a path approximated by the line and passes within 1 au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line
The object enters along a path approximated by the line and passes within 1 au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line
The object It enters along a path approximated by the line and passes within 1 au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?