| << Chapter < Page | Chapter >> Page > |
For the following exercises, use basic identities to simplify the expression.
For the following exercises, determine if the given identities are equivalent.
For the following exercises, find the exact value.
For the following exercises, prove the identity.
For the following exercise, simplify the expression.
For the following exercises, find the exact value.
For the following exercises, find the exact value.
Find and given and is in the interval
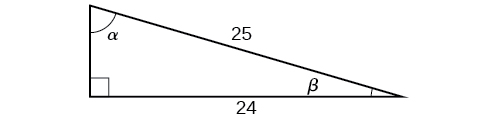
For the following exercises, use [link] to find the desired quantities.
For the following exercises, prove the identity.
For the following exercises, rewrite the expression with no powers.
For the following exercises, evaluate the product for the given expression using a sum or difference of two functions. Write the exact answer.
For the following exercises, evaluate the sum by using a product formula. Write the exact answer.
For the following exercises, change the functions from a product to a sum or a sum to a product.
For the following exercises, find all exact solutions on the interval
For the following exercises, find all exact solutions on the interval

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?