| << Chapter < Page | Chapter >> Page > |
Due to advances in medicine and higher standards of living, life expectancy has been increasing in most developed countries since the beginning of the 20th century.
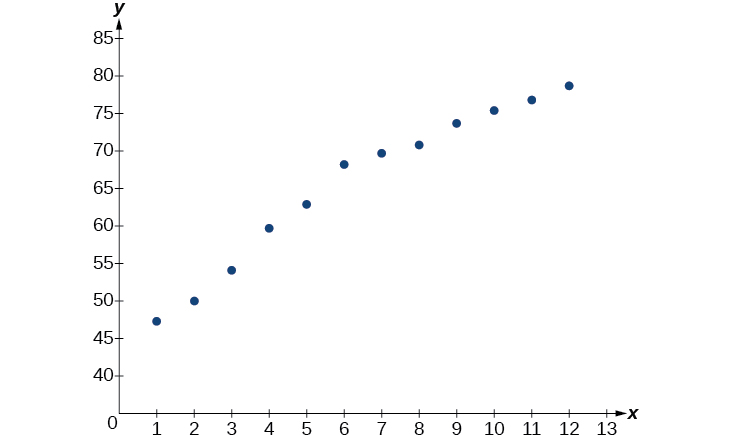
[link] shows the average life expectancies, in years, of Americans from 1900–2010 Source: Center for Disease Control and Prevention, 2013 .
| Year | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 |
| Life Expectancy(Years) | 47.3 | 50.0 | 54.1 | 59.7 | 62.9 | 68.2 |
| Year | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
| Life Expectancy(Years) | 69.7 | 70.8 | 73.7 | 75.4 | 76.8 | 78.7 |
Use the “LnReg” command from the STAT then CALC menu to obtain the logarithmic model,
Next, graph the model in the same window as the scatterplot to verify it is a good fit as shown in [link] :
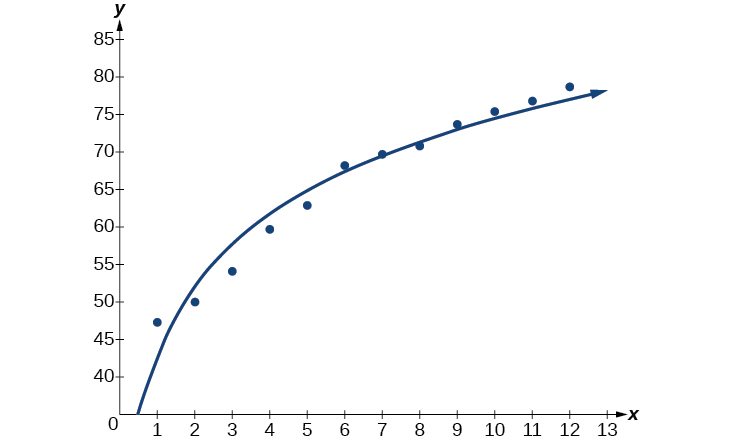
If life expectancy continues to increase at this pace, the average life expectancy of an American will be 79.1 by the year 2030.
Sales of a video game released in the year 2000 took off at first, but then steadily slowed as time moved on. [link] shows the number of games sold, in thousands, from the years 2000–2010.
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Number Sold (thousands) | 142 | 149 | 154 | 155 | 159 | 161 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | - |
| Number Sold (thousands) | 163 | 164 | 164 | 166 | 167 | - |
Like exponential and logarithmic growth, logistic growth increases over time. One of the most notable differences with logistic growth models is that, at a certain point, growth steadily slows and the function approaches an upper bound, or limiting value . Because of this, logistic regression is best for modeling phenomena where there are limits in expansion, such as availability of living space or nutrients.
It is worth pointing out that logistic functions actually model resource-limited exponential growth. There are many examples of this type of growth in real-world situations, including population growth and spread of disease, rumors, and even stains in fabric. When performing logistic regression analysis , we use the form most commonly used on graphing utilities:

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?