| << Chapter < Page | Chapter >> Page > |
Write the first five terms of the sequence.
Substitute and so on in the formula.
The first five terms are
In [link] , does the (–1) to the power of account for the oscillations of signs?
Yes, the power might be and so on, but any odd powers will result in a negative term, and any even power will result in a positive term.
Write the first five terms of the sequence:
The first five terms are
We’ve learned that sequences are functions whose domain is over the positive integers. This is true for other types of functions, including some piecewise functions . Recall that a piecewise function is a function defined by multiple subsections. A different formula might represent each individual subsection.
Given an explicit formula for a piecewise function, write the first terms of a sequence
Write the first six terms of the sequence.
Substitute and so on in the appropriate formula. Use when is not a multiple of 3. Use when is a multiple of 3.
The first six terms are
Write the first six terms of the sequence.
The first six terms are
Thus far, we have been given the explicit formula and asked to find a number of terms of the sequence. Sometimes, the explicit formula for the term of a sequence is not given. Instead, we are given several terms from the sequence. When this happens, we can work in reverse to find an explicit formula from the first few terms of a sequence. The key to finding an explicit formula is to look for a pattern in the terms. Keep in mind that the pattern may involve alternating terms, formulas for numerators, formulas for denominators, exponents, or bases.
Given the first few terms of a sequence, find an explicit formula for the sequence.
Write an explicit formula for the term of each sequence.
Look for the pattern in each sequence.
The terms are all negative.
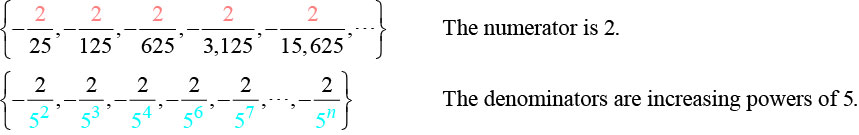
So we know that the fraction is negative, the numerator is 2, and the denominator can be represented by
The terms are powers of For the first term is so the exponent must be

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?