| << Chapter < Page | Chapter >> Page > |
Divide by
We begin by writing the problem as a fraction.
Then we multiply the numerator and denominator by the complex conjugate of the denominator.
To multiply two complex numbers, we expand the product as we would with polynomials (the process commonly called FOIL).
Note that this expresses the quotient in standard form.
Let Evaluate
Substitute into the function and simplify.
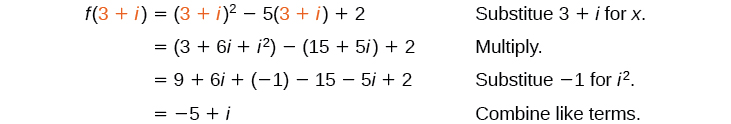
Let Evaluate
Substitute and simplify.
The powers of are cyclic. Let’s look at what happens when we raise to increasing powers.
We can see that when we get to the fifth power of it is equal to the first power. As we continue to multiply by itself for increasing powers, we will see a cycle of 4. Let’s examine the next 4 powers of
Evaluate
Since we can simplify the problem by factoring out as many factors of as possible. To do so, first determine how many times 4 goes into 35:
Can we write in other helpful ways?
As we saw in [link] , we reduced to by dividing the exponent by 4 and using the remainder to find the simplified form. But perhaps another factorization of may be more useful. [link] shows some other possible factorizations.
| Factorization of | ||||
| Reduced form | ||||
| Simplified form |
Each of these will eventually result in the answer we obtained above but may require several more steps than our earlier method.
Access these online resources for additional instruction and practice with complex numbers.
Explain how to add complex numbers.
Add the real parts together and the imaginary parts together.
What is the basic principle in multiplication of complex numbers?
Give an example to show the product of two imaginary numbers is not always imaginary.
times equals –1, which is not imaginary. (answers vary)
What is a characteristic of the plot of a real number in the complex plane?
For the following exercises, evaluate the algebraic expressions.
For the following exercises, determine the number of real and nonreal solutions for each quadratic function shown.
For the following exercises, plot the complex numbers on the complex plane.
For the following exercises, perform the indicated operation and express the result as a simplified complex number.
For the following exercises, use a calculator to help answer the questions.
Evaluate for Predict the value if
Evaluate for . Predict the value for
Show that a solution of is
For the following exercises, evaluate the expressions, writing the result as a simplified complex number.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?