| << Chapter < Page | Chapter >> Page > |
Using the equation in [link] , find the zeros and maximum and, if necessary, the polar axis intercepts of
To find the zeros, set equal to zero and solve for
Substitute any one of the values into the equation. We will use
The points and are the zeros of the equation. They all coincide, so only one point is visible on the graph. This point is also the only polar axis intercept.
To find the maximum value of the equation, look at the maximum value of the trigonometric function which occurs when resulting in Substitute for
Without converting to Cartesian coordinates, test the given equation for symmetry and find the zeros and maximum values of
Tests will reveal symmetry about the polar axis. The zero is and the maximum value is
Now we have seen the equation of a circle in the polar coordinate system. In the last two examples, the same equation was used to illustrate the properties of symmetry and demonstrate how to find the zeros, maximum values, and plotted points that produced the graphs. However, the circle is only one of many shapes in the set of polar curves.
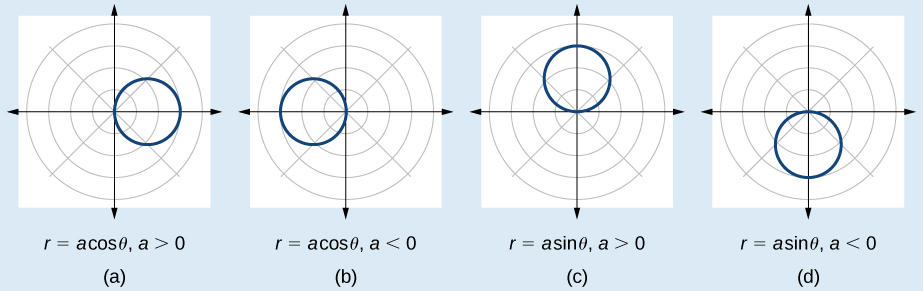
There are five classic polar curves : cardioids , limaҫons, lemniscates, rose curves , and Archimedes’ spirals . We will briefly touch on the polar formulas for the circle before moving on to the classic curves and their variations.
Some of the formulas that produce the graph of a circle in polar coordinates are given by and where is the diameter of the circle or the distance from the pole to the farthest point on the circumference. The radius is or one-half the diameter. For the center is For the center is [link] shows the graphs of these four circles.
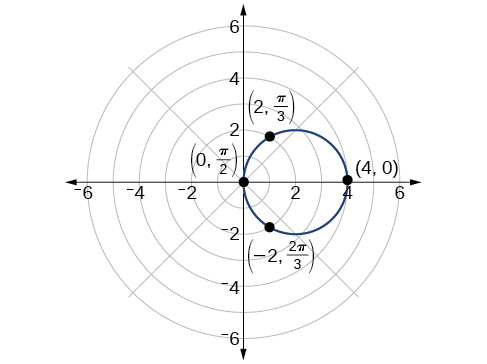
Sketch the graph of
First, testing the equation for symmetry, we find that the graph is symmetric about the polar axis. Next, we find the zeros and maximum for First, set and solve for . Thus, a zero occurs at A key point to plot is
To find the maximum value of note that the maximum value of the cosine function is 1 when Substitute into the equation:
The maximum value of the equation is 4. A key point to plot is
As is symmetric with respect to the polar axis, we only need to calculate r -values for over the interval Points in the upper quadrant can then be reflected to the lower quadrant. Make a table of values similar to [link] . The graph is shown in [link] .
| 0 | |||||||||
| 4 | 3.46 | 2.83 | 2 | 0 | −2 | −2.83 | −3.46 | 4 |
While translating from polar coordinates to Cartesian coordinates may seem simpler in some instances, graphing the classic curves is actually less complicated in the polar system. The next curve is called a cardioid, as it resembles a heart. This shape is often included with the family of curves called limaçons, but here we will discuss the cardioid on its own.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?