| << Chapter < Page | Chapter >> Page > |
| Binomial Theorem | |
| term of a binomial expansion |
What is a binomial coefficient, and how it is calculated?
A binomial coefficient is an alternative way of denoting the combination It is defined as
What role do binomial coefficients play in a binomial expansion? Are they restricted to any type of number?
What is the Binomial Theorem and what is its use?
The Binomial Theorem is defined as and can be used to expand any binomial.
When is it an advantage to use the Binomial Theorem? Explain.
For the following exercises, evaluate the binomial coefficient.
For the following exercises, use the Binomial Theorem to expand each binomial.
For the following exercises, use the Binomial Theorem to write the first three terms of each binomial.
For the following exercises, find the indicated term of each binomial without fully expanding the binomial.
The fourth term of
The third term of
The seventh term of
The tenth term of
The fourth term of
For the following exercises, use the Binomial Theorem to expand the binomial Then find and graph each indicated sum on one set of axes.
Find and graph such that is the first term of the expansion.
Find and graph such that is the sum of the first two terms of the expansion.
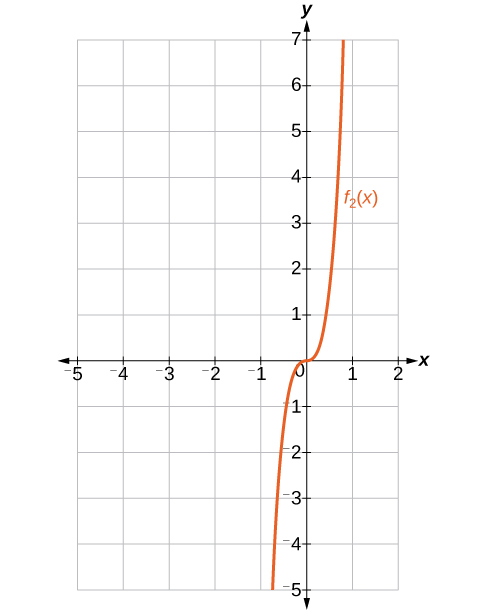
Find and graph such that is the sum of the first three terms of the expansion.
Find and graph such that is the sum of the first four terms of the expansion.
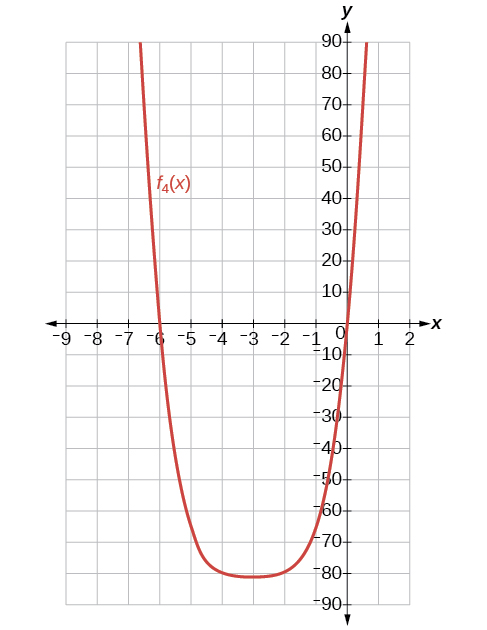
Find and graph such that is the sum of the first five terms of the expansion.
In the expansion of each term has the form successively takes on the value If what is the corresponding term?
In the expansion of the coefficient of is the same as the coefficient of which other term?
Consider the expansion of What is the exponent of in the term?
Find and write the answer as a binomial coefficient in the form Prove it. Hint: Use the fact that, for any integer such that
Proof:
Which expression cannot be expanded using the Binomial Theorem? Explain.
The expression cannot be expanded using the Binomial Theorem because it cannot be rewritten as a binomial.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?