| << Chapter < Page | Chapter >> Page > |
The polar form of a complex number expresses a number in terms of an angle and its distance from the origin Given a complex number in rectangular form expressed as we use the same conversion formulas as we do to write the number in trigonometric form:
We review these relationships in [link] .
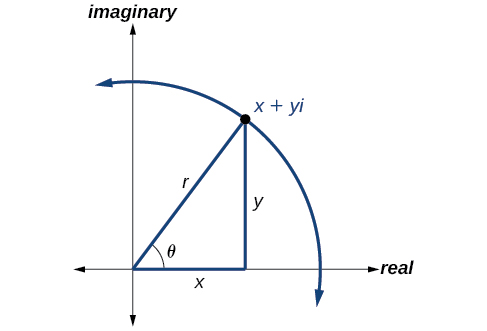
We use the term modulus to represent the absolute value of a complex number, or the distance from the origin to the point The modulus, then, is the same as the radius in polar form. We use to indicate the angle of direction (just as with polar coordinates). Substituting, we have
Writing a complex number in polar form involves the following conversion formulas:
Making a direct substitution, we have
where is the modulus and is the argument . We often use the abbreviation to represent
Express the complex number using polar coordinates.
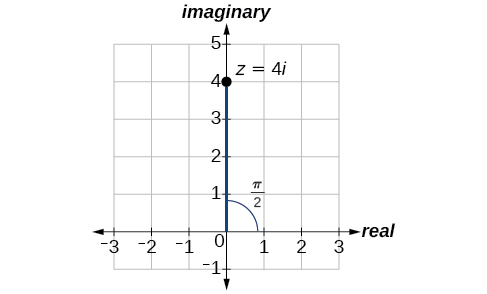
On the complex plane, the number is the same as Writing it in polar form, we have to calculate first.
Next, we look at If and then In polar coordinates, the complex number can be written as or See [link] .
Find the polar form of
First, find the value of
Find the angle using the formula:
Thus, the solution is
Converting a complex number from polar form to rectangular form is a matter of evaluating what is given and using the distributive property. In other words, given first evaluate the trigonometric functions and Then, multiply through by
Convert the polar form of the given complex number to rectangular form:
We begin by evaluating the trigonometric expressions.
After substitution, the complex number is
We apply the distributive property:
The rectangular form of the given point in complex form is
Find the rectangular form of the complex number given and
If and we first determine We then find and
The rectangular form of the given number in complex form is
Now that we can convert complex numbers to polar form we will learn how to perform operations on complex numbers in polar form. For the rest of this section, we will work with formulas developed by French mathematician Abraham de Moivre (1667-1754). These formulas have made working with products, quotients, powers, and roots of complex numbers much simpler than they appear. The rules are based on multiplying the moduli and adding the arguments.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?