| << Chapter < Page | Chapter >> Page > |
To evaluate an exponential function with the form we simply substitute with the given value, and calculate the resulting power. For example:
Let What is
To evaluate an exponential function with a form other than the basic form, it is important to follow the order of operations. For example:
Let What is
Note that if the order of operations were not followed, the result would be incorrect:
Let Evaluate without using a calculator.
Follow the order of operations. Be sure to pay attention to the parentheses.
Let Evaluate using a calculator. Round to four decimal places.
Because the output of exponential functions increases very rapidly, the term “exponential growth” is often used in everyday language to describe anything that grows or increases rapidly. However, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.
A function that models exponential growth grows by a rate proportional to the amount present. For any real number and any positive real numbers and such that an exponential growth function has the form
where
In more general terms, we have an exponential function , in which a constant base is raised to a variable exponent. To differentiate between linear and exponential functions, let’s consider two companies, A and B. Company A has 100 stores and expands by opening 50 new stores a year, so its growth can be represented by the function Company B has 100 stores and expands by increasing the number of stores by 50% each year, so its growth can be represented by the function
A few years of growth for these companies are illustrated in [link] .
| Year, | Stores, Company A | Stores, Company B |
|---|---|---|
The graphs comparing the number of stores for each company over a five-year period are shown in [link] . We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
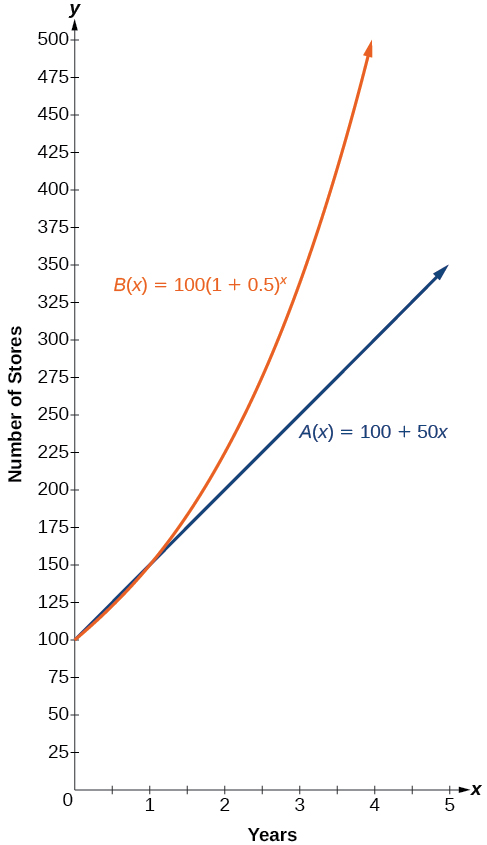
Notice that the domain for both functions is and the range for both functions is After year 1, Company B always has more stores than Company A.
Now we will turn our attention to the function representing the number of stores for Company B, In this exponential function, 100 represents the initial number of stores, 0.50 represents the growth rate, and represents the growth factor. Generalizing further, we can write this function as where 100 is the initial value, is called the base , and is called the exponent .

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?