| << Chapter < Page | Chapter >> Page > |
Bicycle ramps made for competition (see [link] ) must vary in height depending on the skill level of the competitors. For advanced competitors, the angle formed by the ramp and the ground should be such that The angle is divided in half for novices. What is the steepness of the ramp for novices? In this section, we will investigate three additional categories of identities that we can use to answer questions such as this one.
In the previous section, we used addition and subtraction formulas for trigonometric functions. Now, we take another look at those same formulas. The double-angle formulas are a special case of the sum formulas, where Deriving the double-angle formula for sine begins with the sum formula,
If we let then we have
Deriving the double-angle for cosine gives us three options. First, starting from the sum formula, and letting we have
Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more interpretations. The first one is:
The second interpretation is:
Similarly, to derive the double-angle formula for tangent, replacing in the sum formula gives
The double-angle formulas are summarized as follows:
Given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value.
Given that and is in quadrant II, find the following:
If we draw a triangle to reflect the information given, we can find the values needed to solve the problems on the image. We are given such that is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because is in the second quadrant, the adjacent side is on the x -axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:
Now we can draw a triangle similar to the one shown in [link] .
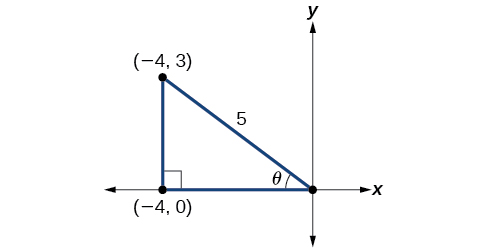
We see that we to need to find and Based on [link] , we see that the hypotenuse equals 5, so and Substitute these values into the equation, and simplify.
Thus,
Again, substitute the values of the sine and cosine into the equation, and simplify.
In this formula, we need the tangent, which we were given as Substitute this value into the equation, and simplify.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?