| << Chapter < Page | Chapter >> Page > |
Discuss why this statement is incorrect: for all
Determine whether the following statement is true or false and explain your answer:
True . The angle, that equals , , will be a second quadrant angle with reference angle, , where equals , . Since is the reference angle for , and = -
For the following exercises, evaluate the expressions.
For the following exercises, use a calculator to evaluate each expression. Express answers to the nearest hundredth.
For the following exercises, find the angle in the given right triangle. Round answers to the nearest hundredth.
For the following exercises, find the exact value, if possible, without a calculator. If it is not possible, explain why.
For the following exercises, find the exact value of the expression in terms of with the help of a reference triangle.
For the following exercises, evaluate the expression without using a calculator. Give the exact value.
For the following exercises, find the function if
Graph and state the domain and range of the function.
Graph and state the domain and range of the function.
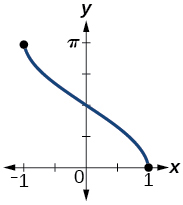
domain range
Graph one cycle of and state the domain and range of the function.
For what value of does Use a graphing calculator to approximate the answer.
approximately
For what value of does Use a graphing calculator to approximate the answer.
Suppose a 13-foot ladder is leaning against a building, reaching to the bottom of a second-floor window 12 feet above the ground. What angle, in radians, does the ladder make with the building?
0.395 radians
Suppose you drive 0.6 miles on a road so that the vertical distance changes from 0 to 150 feet. What is the angle of elevation of the road?
An isosceles triangle has two congruent sides of length 9 inches. The remaining side has a length of 8 inches. Find the angle that a side of 9 inches makes with the 8-inch side.
1.11 radians
Without using a calculator, approximate the value of Explain why your answer is reasonable.
A truss for the roof of a house is constructed from two identical right triangles. Each has a base of 12 feet and height of 4 feet. Find the measure of the acute angle adjacent to the 4-foot side.
1.25 radians

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?