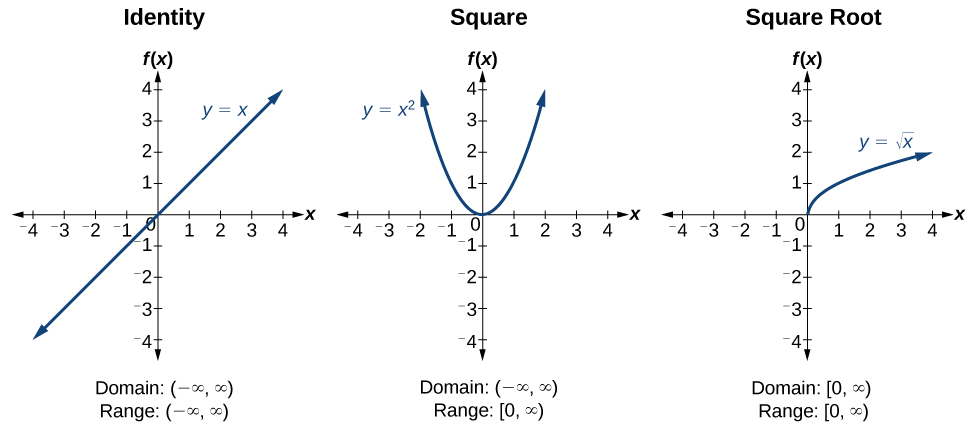
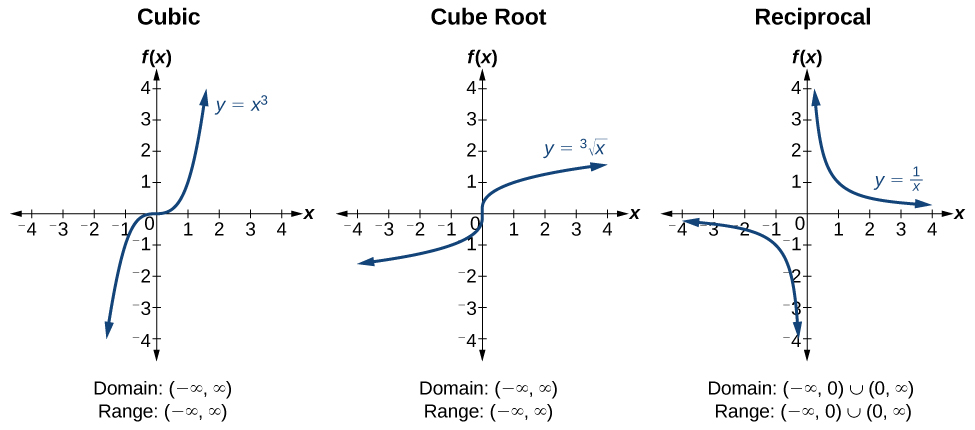
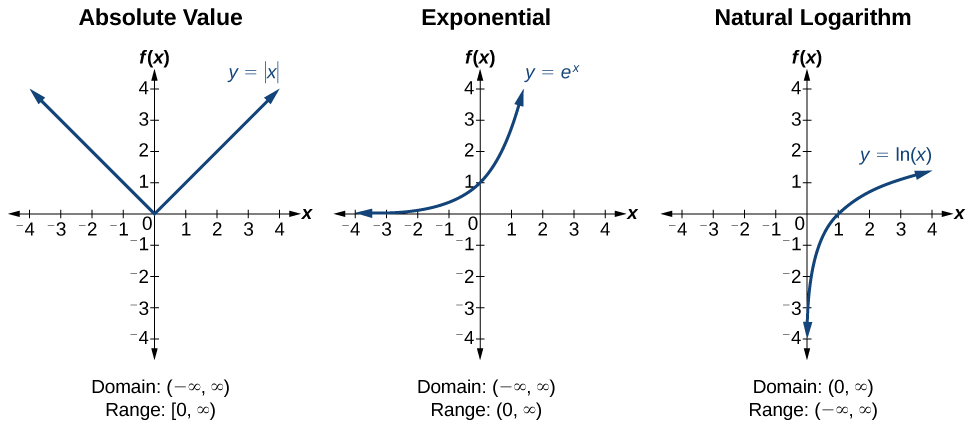
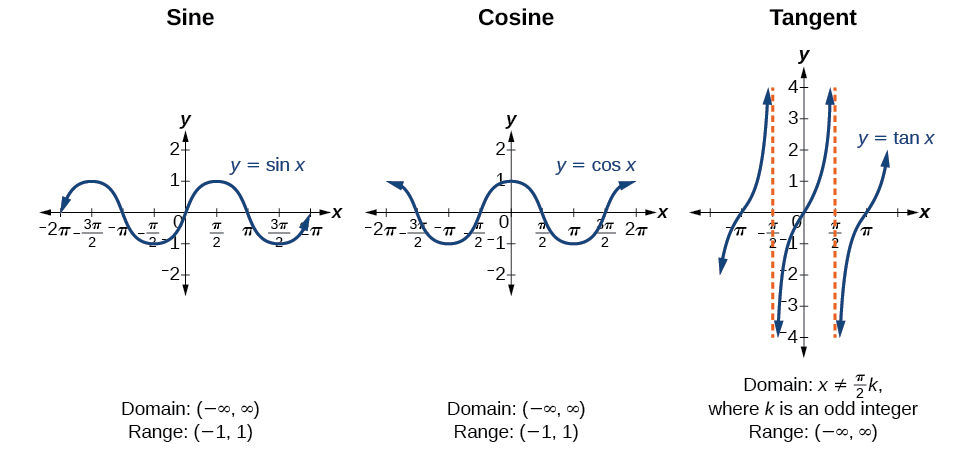
| Pythagorean Identities |
|
| Even-Odd Identities |
|
| Cofunction Identities |
|
| Fundamental Identities |
|
| Sum and Difference Identities |
|
| Double-Angle Formulas |
|
| Half-Angle Formulas |
|
| Reduction Formulas |
|
| Product-to-Sum Formulas |
|
| Sum-to-Product Formulas |
|
| Law of Sines |
|
| Law of Cosines |
|