| << Chapter < Page | Chapter >> Page > |
As the charge on the capacitor increases, the current through the resistor decreases, as shown in [link] (b). The current through the resistor can be found by taking the time derivative of the charge.
At time the current through the resistor is . As time approaches infinity, the current approaches zero. At time , the current through the resistor is
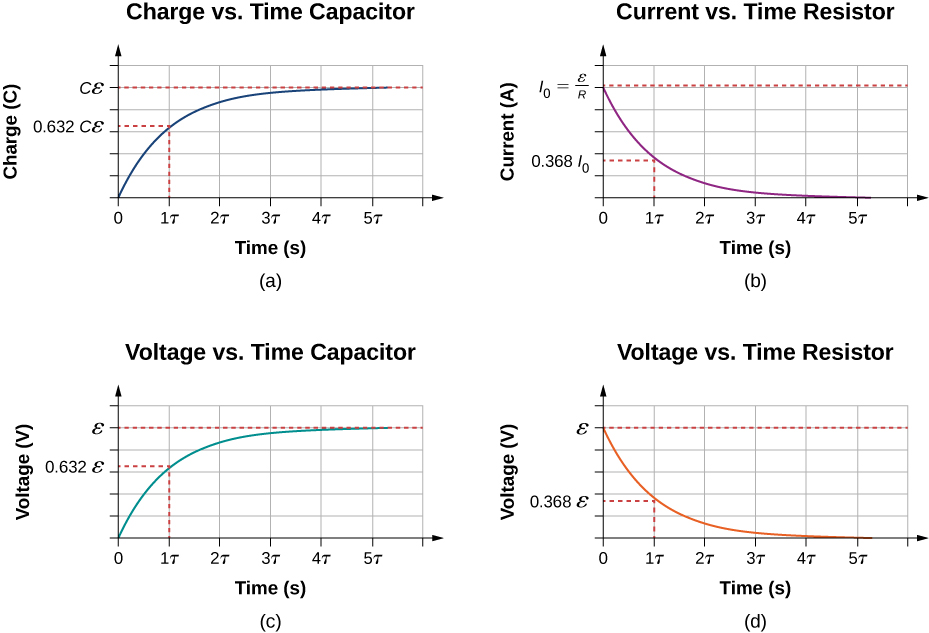
[link] (c) and [link] (d) show the voltage differences across the capacitor and the resistor, respectively. As the charge on the capacitor increases, the current decreases, as does the voltage difference across the resistor The voltage difference across the capacitor increases as
When the switch in [link] (a) is moved to position B , the circuit reduces to the circuit in part (c), and the charged capacitor is allowed to discharge through the resistor. A graph of the charge on the capacitor as a function of time is shown in [link] (a). Using Kirchhoff’s loop rule to analyze the circuit as the capacitor discharges results in the equation , which simplifies to . Using the definition of current and integrating the loop equation yields an equation for the charge on the capacitor as a function of time:
Here, Q is the initial charge on the capacitor and is the time constant of the circuit. As shown in the graph, the charge decreases exponentially from the initial charge, approaching zero as time approaches infinity.
The current as a function of time can be found by taking the time derivative of the charge:
The negative sign shows that the current flows in the opposite direction of the current found when the capacitor is charging. [link] (b) shows an example of a plot of charge versus time and current versus time. A plot of the voltage difference across the capacitor and the voltage difference across the resistor as a function of time are shown in parts (c) and (d) of the figure. Note that the magnitudes of the charge, current, and voltage all decrease exponentially, approaching zero as time increases.
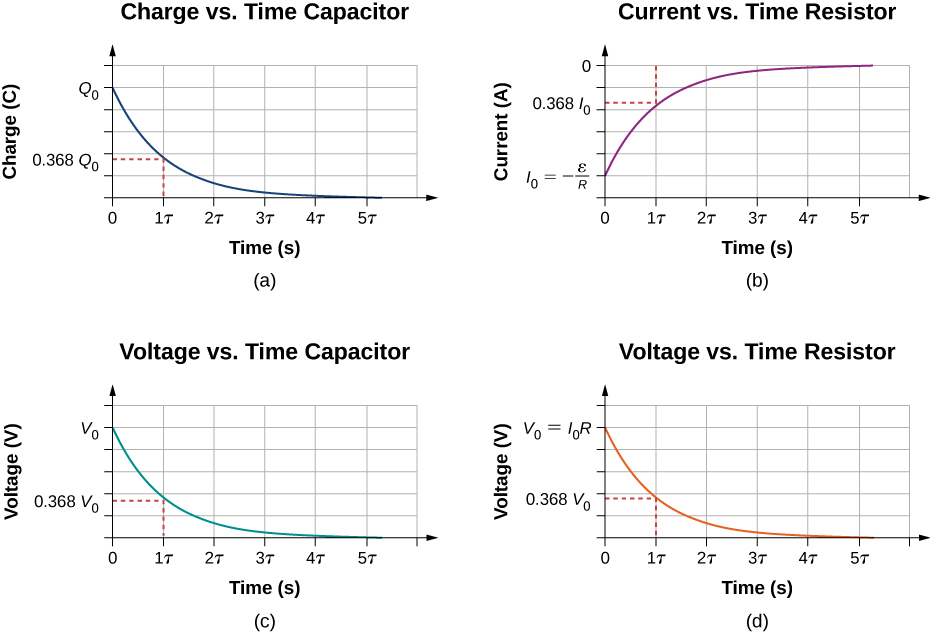
Now we can explain why the flash camera mentioned at the beginning of this section takes so much longer to charge than discharge: The resistance while charging is significantly greater than while discharging. The internal resistance of the battery accounts for most of the resistance while charging. As the battery ages, the increasing internal resistance makes the charging process even slower.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?