| << Chapter < Page | Chapter >> Page > |
A note about symbols: We use for locating charges in the charge distribution and r for locating the field point(s) at the Gaussian surface(s). The letter R is used for the radius of the charge distribution.
As charge density is not constant here, we need to integrate the charge density function over the volume enclosed by the Gaussian surface. Therefore, we set up the problem for charges in one spherical shell, say between and as shown in [link] . The volume of charges in the shell of infinitesimal width is equal to the product of the area of surface and the thickness . Multiplying the volume with the density at this location, which is , gives the charge in the shell:
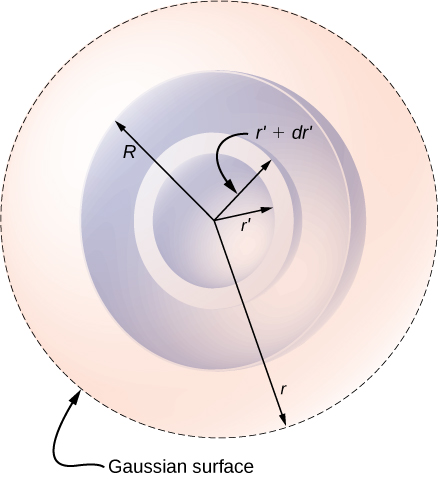
(a) Field at a point outside the charge distribution. In this case, the Gaussian surface, which contains the field point P , has a radius r that is greater than the radius R of the charge distribution, . Therefore, all charges of the charge distribution are enclosed within the Gaussian surface. Note that the space between and is empty of charges and therefore does not contribute to the integral over the volume enclosed by the Gaussian surface:
This is used in the general result for above to obtain the electric field at a point outside the charge distribution as
where is a unit vector in the direction from the origin to the field point at the Gaussian surface.
(b) Field at a point inside the charge distribution. The Gaussian surface is now buried inside the charge distribution, with . Therefore, only those charges in the distribution that are within a distance r of the center of the spherical charge distribution count in :
Now, using the general result above for we find the electric field at a point that is a distance r from the center and lies within the charge distribution as

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?