| << Chapter < Page | Chapter >> Page > |
James Clerk Maxwell (1831–1879) was one of the major contributors to physics in the nineteenth century ( [link] ). Although he died young, he made major contributions to the development of the kinetic theory of gases, to the understanding of color vision, and to the nature of Saturn’s rings. He is probably best known for having combined existing knowledge of the laws of electricity and of magnetism with insights of his own into a complete overarching electromagnetic theory, represented by Maxwell’s equations .

The four basic laws of electricity and magnetism had been discovered experimentally through the work of physicists such as Oersted, Coulomb, Gauss, and Faraday. Maxwell discovered logical inconsistencies in these earlier results and identified the incompleteness of Ampère’s law as their cause.
Recall that according to Ampère’s law, the integral of the magnetic field around a closed loop C is proportional to the current I passing through any surface whose boundary is loop C itself:
There are infinitely many surfaces that can be attached to any loop, and Ampère’s law stated in [link] is independent of the choice of surface.
Consider the set-up in [link] . A source of emf is abruptly connected across a parallel-plate capacitor so that a time-dependent current I develops in the wire. Suppose we apply Ampère’s law to loop C shown at a time before the capacitor is fully charged, so that . Surface gives a nonzero value for the enclosed current I , whereas surface gives zero for the enclosed current because no current passes through it:
Clearly, Ampère’s law in its usual form does not work here. This may not be surprising, because Ampère’s law as applied in earlier chapters required a steady current, whereas the current in this experiment is changing with time and is not steady at all.
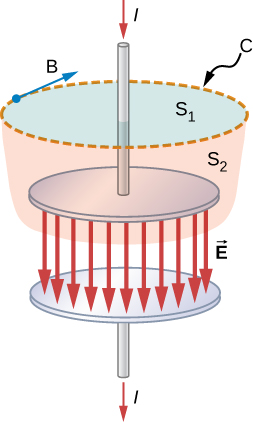
How can Ampère’s law be modified so that it works in all situations? Maxwell suggested including an additional contribution, called the displacement current , to the real current I ,
where the displacement current is defined to be
Here is the permittivity of free space and is the electric flux , defined as
The displacement current is analogous to a real current in Ampère’s law, entering into Ampère’s law in the same way. It is produced, however, by a changing electric field. It accounts for a changing electric field producing a magnetic field, just as a real current does, but the displacement current can produce a magnetic field even where no real current is present. When this extra term is included, the modified Ampère’s law equation becomes

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?