| << Chapter < Page | Chapter >> Page > |
In the discussion of vector addition we saw that a number of vectors acting together can be combined to give a single vector (the resultant). Inmuch the same way a single vector can be broken down into a number of vectors which when added give that original vector. These vectors which sum to the original are called components of the original vector. The process of breaking a vector into its components is called resolving into components .
While summing a given set of vectors gives just one answer (the resultant), a single vector can be resolved into infinitely many setsof components. In the diagrams below the same black vector is resolved into different pairs of components. These components are shown as dashed lines. When added together the dashed vectors give the original black vector(i.e. the original vector is the resultant of its components).
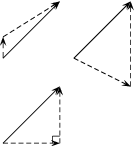
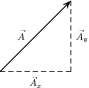
In practice it is most useful to resolve a vector into components which are at right angles to one another, usually horizontal and vertical.
Any vector can be resolved into a horizontal and a vertical component. If is a vector, then the horizontal component of is and the vertical component is .
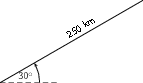
A motorist undergoes a displacement of 250 km in a direction 30 north of east. Resolve this displacement into components in the directions north ( ) and east ( ).
Next we resolve the displacement into its components north and east. Since these directions are perpendicular to one another, thecomponents form a right-angled triangle with the original displacement as its hypotenuse.
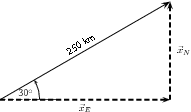
Notice how the two components acting together give the original vector as their resultant.
Now we can use trigonometry to calculate the magnitudes of the components of the original displacement:
and
Remember and are the magnitudes of the components – they are in the directions north and east respectively.
As a further example of components let us consider a block of mass placed on a frictionless surface inclined at some angle to the horizontal. The block will obviously slide down the incline, butwhat causes this motion?
The forces acting on the block are its weight and the normal force exerted by the surface on the object. These two forces are shown in the diagram below.
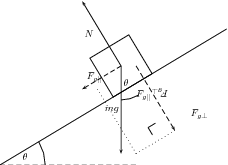
Now the object's weight can be resolved into components parallel and perpendicular to the inclined surface. These components are shown asdashed arrows in the diagram above and are at right angles to each other. The components have been drawn acting from the samepoint. Applying the parallelogram method, the two components of the block's weight sum to the weight vector.
To find the components in terms of the weight we can use trigonometry:
The component of the weight perpendicular to the slope exactly balances the normal force exerted by the surface. The parallel component, however, is unbalanced and causes the block to slide down the slope.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?