| << Chapter < Page | Chapter >> Page > |
so the infinitesimal work element becomes
The integral of is , so the work done from A to B is
As expected, this is exactly the same result as before.
One very important and widely applicable variable force is the force exerted by a perfectly elastic spring, which satisfies Hooke’s law where k is the spring constant, and is the displacement from the spring’s unstretched (equilibrium) position ( Newton’s Laws of Motion ). Note that the unstretched position is only the same as the equilibrium position if no other forces are acting (or, if they are, they cancel one another). Forces between molecules, or in any system undergoing small displacements from a stable equilibrium, behave approximately like a spring force.
To calculate the work done by a spring force, we can choose the x -axis along the length of the spring, in the direction of increasing length, as in [link] , with the origin at the equilibrium position (Then positive x corresponds to a stretch and negative x to a compression.) With this choice of coordinates, the spring force has only an x -component, , and the work done when x changes from to is
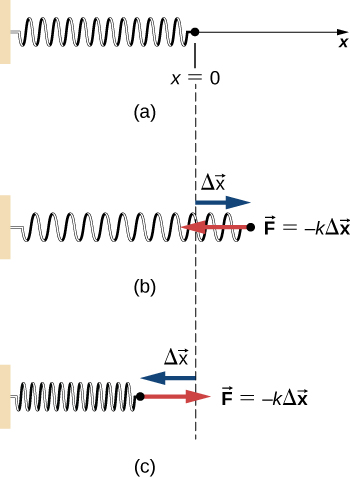
Notice that depends only on the starting and ending points, A and B , and is independent of the actual path between them, as long as it starts at A and ends at B. That is, the actual path could involve going back and forth before ending.
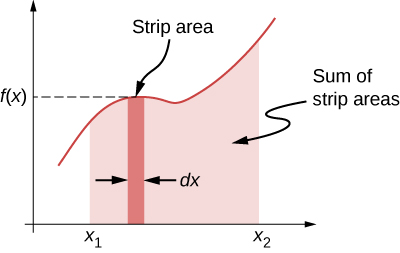
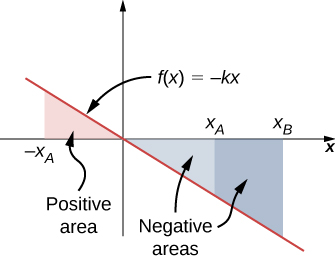
Another interesting thing to notice about [link] is that, for this one-dimensional case, you can readily see the correspondence between the work done by a force and the area under the curve of the force versus its displacement. Recall that, in general, a one-dimensional integral is the limit of the sum of infinitesimals, , representing the area of strips, as shown in [link] . In [link] , since is a straight line with slope , when plotted versus x , the “area” under the line is just an algebraic combination of triangular “areas,” where “areas” above the x -axis are positive and those below are negative, as shown in [link] . The magnitude of one of these “areas” is just one-half the triangle’s base, along the x -axis, times the triangle’s height, along the force axis. (There are quotation marks around “area” because this base-height product has the units of work, rather than square meters.)

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?