| << Chapter < Page | Chapter >> Page > |
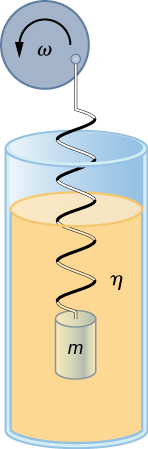
Using Newton’s second law we can analyze the motion of the mass. The resulting equation is similar to the force equation for the damped harmonic oscillator, with the addition of the driving force:
When an oscillator is forced with a periodic driving force, the motion may seem chaotic. The motions of the oscillator is known as transients. After the transients die out, the oscillator reaches a steady state, where the motion is periodic. After some time, the steady state solution to this differential equation is
Once again, it is left as an exercise to prove that this equation is a solution. Taking the first and second time derivative of x ( t ) and substituting them into the force equation shows that is a solution as long as the amplitude is equal to
where is the natural angular frequency of the system of the mass and spring. Recall that the angular frequency, and therefore the frequency, of the motor can be adjusted. Looking at the denominator of the equation for the amplitude, when the driving frequency is much smaller, or much larger, than the natural frequency, the square of the difference of the two angular frequencies is positive and large, making the denominator large, and the result is a small amplitude for the oscillations of the mass. As the frequency of the driving force approaches the natural frequency of the system, the denominator becomes small and the amplitude of the oscillations becomes large. The maximum amplitude results when the frequency of the driving force equals the natural frequency of the system .
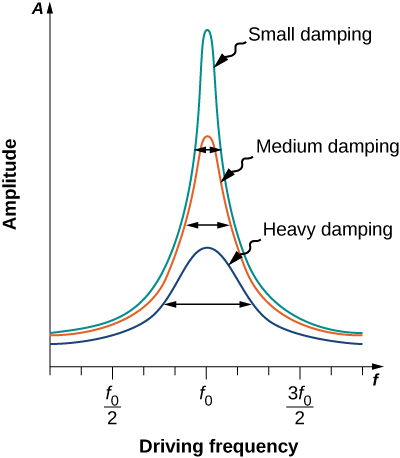
[link] shows a graph of the amplitude of a damped harmonic oscillator as a function of the frequency of the periodic force driving it. Each of the three curves on the graph represents a different amount of damping. All three curves peak at the point where the frequency of the driving force equals the natural frequency of the harmonic oscillator. The highest peak, or greatest response, is for the least amount of damping, because less energy is removed by the damping force. Note that since the amplitude grows as the damping decreases, taking this to the limit where there is no damping , the amplitude becomes infinite.
Note that a small-amplitude driving force can produce a large-amplitude response. This phenomenon is known as resonance. A common example of resonance is a parent pushing a small child on a swing. When the child wants to go higher, the parent does not move back and then, getting a running start, slam into the child, applying a great force in a short interval. Instead, the parent applies small pushes to the child at just the right frequency, and the amplitude of the child’s swings increases.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?