| << Chapter < Page | Chapter >> Page > |
becomes
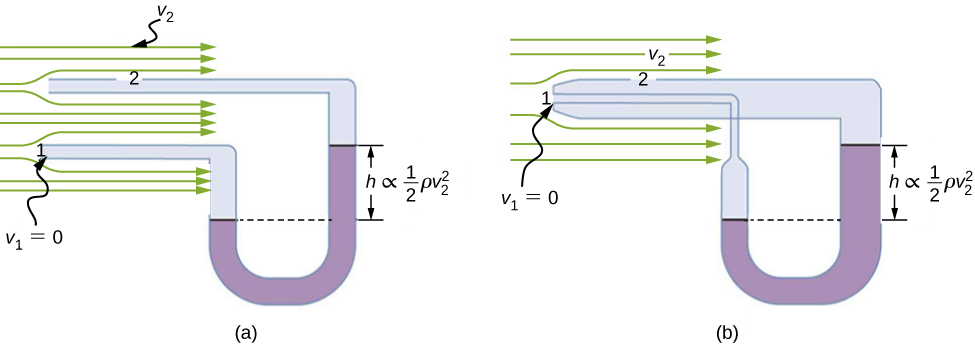
Thus pressure over the second opening is reduced by , so the fluid in the manometer rises by h on the side connected to the second opening, where
(Recall that the symbol means “proportional to.”) Solving for , we see that
Part (b) shows a version of this device that is in common use for measuring various fluid velocities; such devices are frequently used as air-speed indicators in aircraft.
All preceding applications of Bernoulli’s equation involved simplifying conditions, such as constant height or constant pressure. The next example is a more general application of Bernoulli’s equation in which pressure, velocity, and height all change.
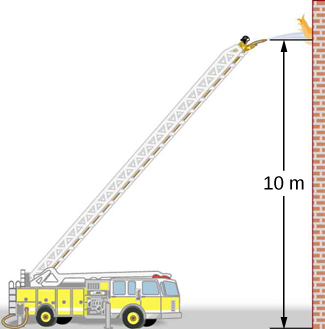
where subscripts 1 and 2 refer to the initial conditions at ground level and the final conditions inside the nozzle, respectively. We must first find the speeds and . Since , we get
Similarly, we find
This rather large speed is helpful in reaching the fire. Now, taking to be zero, we solve Bernoulli’s equation for :
Substituting known values yields

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?