| << Chapter < Page | Chapter >> Page > |
where net means total. Torques, which are in opposite directions are assigned opposite signs. A common convention is to call counterclockwise (ccw) torques positive and clockwise (cw) torques negative.
When two children balance a seesaw as shown in [link] , they satisfy the two conditions for equilibrium. Most people have perfect intuition about seesaws, knowing that the lighter child must sit farther from the pivot and that a heavier child can keep a lighter one off the ground indefinitely.
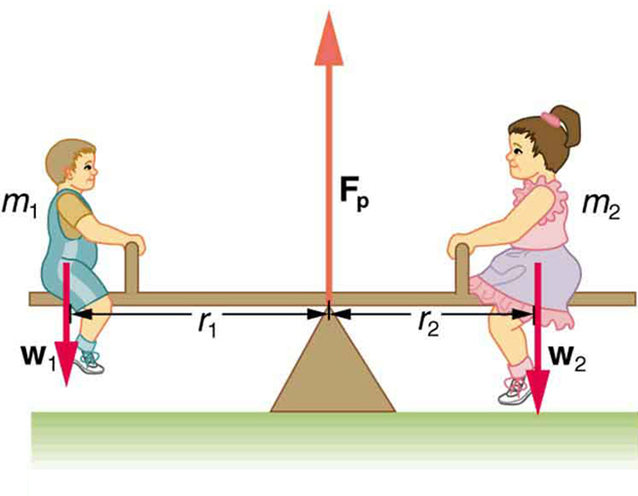
The two children shown in [link] are balanced on a seesaw of negligible mass. (This assumption is made to keep the example simple—more involved examples will follow.) The first child has a mass of 26.0 kg and sits 1.60 m from the pivot.(a) If the second child has a mass of 32.0 kg, how far is she from the pivot? (b) What is , the supporting force exerted by the pivot?
Strategy
Both conditions for equilibrium must be satisfied. In part (a), we are asked for a distance; thus, the second condition (regarding torques) must be used, since the first (regarding only forces) has no distances in it. To apply the second condition for equilibrium, we first identify the system of interest to be the seesaw plus the two children. We take the supporting pivot to be the point about which the torques are calculated. We then identify all external forces acting on the system.
Solution (a)
The three external forces acting on the system are the weights of the two children and the supporting force of the pivot. Let us examine the torque produced by each. Torque is defined to be
Here , so that for all three forces. That means for all three. The torques exerted by the three forces are first,
second,
and third,
Note that a minus sign has been inserted into the second equation because this torque is clockwise and is therefore negative by convention. Since acts directly on the pivot point, the distance is zero. A force acting on the pivot cannot cause a rotation, just as pushing directly on the hinges of a door will not cause it to rotate. Now, the second condition for equilibrium is that the sum of the torques on both children is zero. Therefore
or
Weight is mass times the acceleration due to gravity. Entering for , we get
Solve this for the unknown :
The quantities on the right side of the equation are known; thus, is
As expected, the heavier child must sit closer to the pivot (1.30 m versus 1.60 m) to balance the seesaw.
Solution (b)
This part asks for a force . The easiest way to find it is to use the first condition for equilibrium, which is
The forces are all vertical, so that we are dealing with a one-dimensional problem along the vertical axis; hence, the condition can be written as

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?