| << Chapter < Page | Chapter >> Page > |
The kinetic energy of the atoms in a monatomic ideal gas is its only form of internal energy, and so its total internal energy is
where is the number of atoms in the gas. This relationship means that the internal energy of an ideal monatomic gas is constant during an isothermal process—that is, . If the internal energy does not change, then the net heat transfer into the gas must equal the net work done by the gas. That is, because here, . We must have just enough heat transfer to replace the work done. An isothermal process is inherently slow, because heat transfer occurs continuously to keep the gas temperature constant at all times and must be allowed to spread through the gas so that there are no hot or cold regions.
Also shown in [link] (a) is a curve AC for an adiabatic process, defined to be one in which there is no heat transfer—that is, . Processes that are nearly adiabatic can be achieved either by using very effective insulation or by performing the process so fast that there is little time for heat transfer. Temperature must decrease during an adiabatic process, since work is done at the expense of internal energy:
(You might have noted that a gas released into atmospheric pressure from a pressurized cylinder is substantially colder than the gas in the cylinder.) In fact, because for an adiabatic process. Lower temperature results in lower pressure along the way, so that curve AC is lower than curve AB, and less work is done. If the path ABCA could be followed by cooling the gas from B to C at constant volume (isochorically), [link] (b), there would be a net work output.
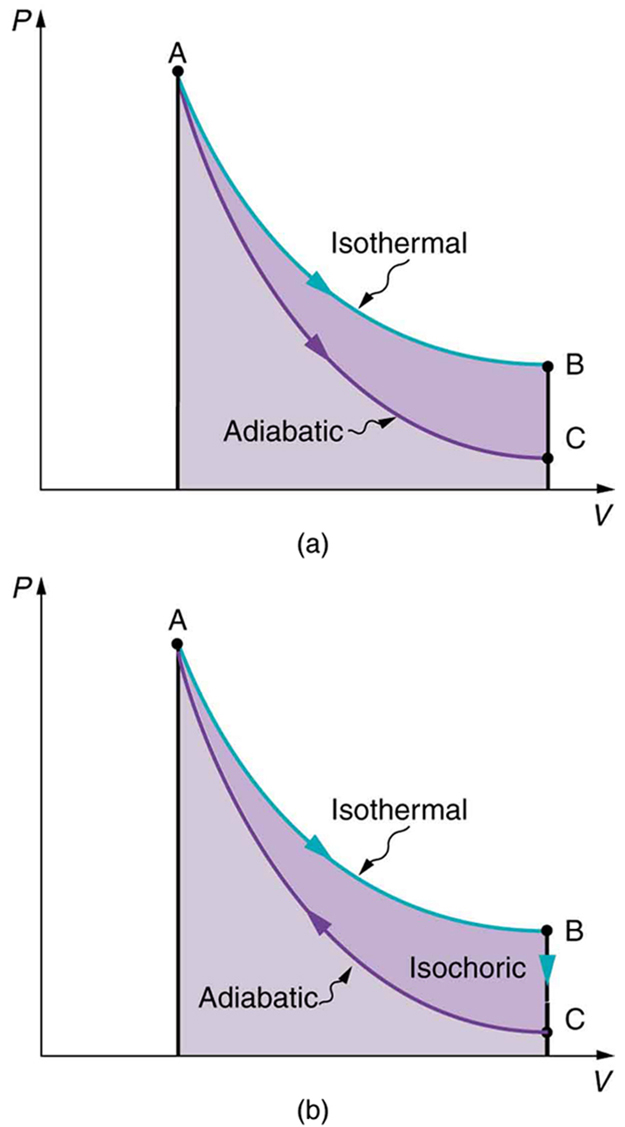
Both isothermal and adiabatic processes such as shown in [link] are reversible in principle. A reversible process is one in which both the system and its environment can return to exactly the states they were in by following the reverse path. The reverse isothermal and adiabatic paths are BA and CA, respectively. Real macroscopic processes are never exactly reversible. In the previous examples, our system is a gas (like that in [link] ), and its environment is the piston, cylinder, and the rest of the universe. If there are any energy-dissipating mechanisms, such as friction or turbulence, then heat transfer to the environment occurs for either direction of the piston. So, for example, if the path BA is followed and there is friction, then the gas will be returned to its original state but the environment will not—it will have been heated in both directions. Reversibility requires the direction of heat transfer to reverse for the reverse path. Since dissipative mechanisms cannot be completely eliminated, real processes cannot be reversible.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?