| << Chapter < Page | Chapter >> Page > |
Matter and photons are waves, implying they are spread out over some distance. What is the position of a particle, such as an electron? Is it at the center of the wave? The answer lies in how you measure the position of an electron. Experiments show that you will find the electron at some definite location, unlike a wave. But if you set up exactly the same situation and measure it again, you will find the electron in a different location, often far outside any experimental uncertainty in your measurement. Repeated measurements will display a statistical distribution of locations that appears wavelike. (See [link] .)
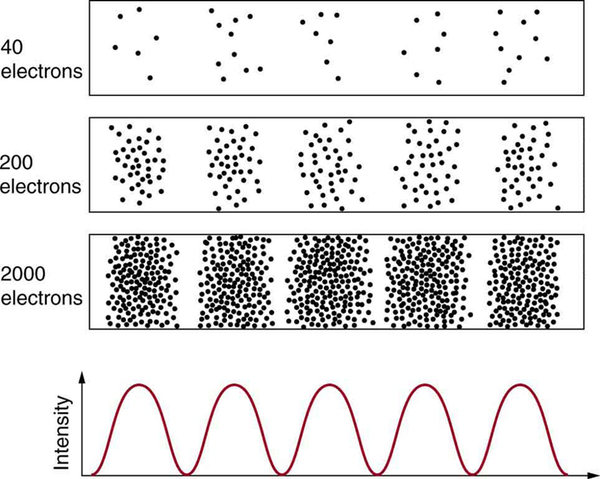

After de Broglie proposed the wave nature of matter, many physicists, including Schrödinger and Heisenberg, explored the consequences. The idea quickly emerged that, because of its wave character, a particle’s trajectory and destination cannot be precisely predicted for each particle individually . However, each particle goes to a definite place (as illustrated in [link] ). After compiling enough data, you get a distribution related to the particle’s wavelength and diffraction pattern. There is a certain probability of finding the particle at a given location, and the overall pattern is called a probability distribution . Those who developed quantum mechanics devised equations that predicted the probability distribution in various circumstances.
It is somewhat disquieting to think that you cannot predict exactly where an individual particle will go, or even follow it to its destination. Let us explore what happens if we try to follow a particle. Consider the double-slit patterns obtained for electrons and photons in [link] . First, we note that these patterns are identical, following , the equation for double-slit constructive interference developed in Photon Energies and the Electromagnetic Spectrum , where is the slit separation and is the electron or photon wavelength.
Both patterns build up statistically as individual particles fall on the detector. This can be observed for photons or electrons—for now, let us concentrate on electrons. You might imagine that the electrons are interfering with one another as any waves do. To test this, you can lower the intensity until there is never more than one electron between the slits and the screen. The same interference pattern builds up! This implies that a particle’s probability distribution spans both slits, and the particles actually interfere with themselves. Does this also mean that the electron goes through both slits? An electron is a basic unit of matter that is not divisible. But it is a fair question, and so we should look to see if the electron traverses one slit or the other, or both. One possibility is to have coils around the slits that detect charges moving through them. What is observed is that an electron always goes through one slit or the other; it does not split to go through both. But there is a catch. If you determine that the electron went through one of the slits, you no longer get a double slit pattern—instead, you get single slit interference. There is no escape by using another method of determining which slit the electron went through. Knowing the particle went through one slit forces a single-slit pattern. If you do not observe which slit the electron goes through, you obtain a double-slit pattern.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?