1. Home
  2. College physics
  3. Electromagnetic induction, ac
  4. Rlc series ac circuits

23.12 Rlc series ac circuits  (Page 3/9)

<< Chapter < Page
  College physics     Page 3 / 9
Chapter >> Page >

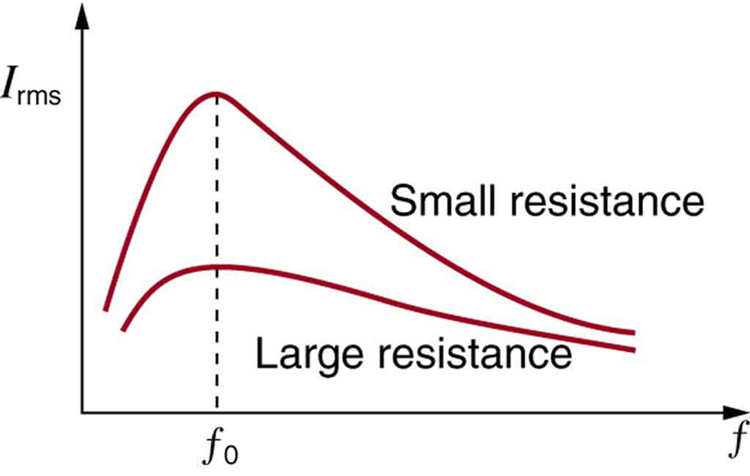
Resonance in AC circuits is analogous to mechanical resonance, where resonance is defined to be a forced oscillation—in this case, forced by the voltage source—at the natural frequency of the system. The receiver in a radio is an RLC circuit that oscillates best at its f 0 size 12{f rSub { size 8{0} } } {} . A variable capacitor is often used to adjust f 0 size 12{f rSub { size 8{0} } } {} to receive a desired frequency and to reject others. [link] is a graph of current as a function of frequency, illustrating a resonant peak in I rms size 12{I rSub { size 8{"rms"} } } {} at f 0 size 12{f rSub { size 8{0} } } {} . The two curves are for two different circuits, which differ only in the amount of resistance in them. The peak is lower and broader for the higher-resistance circuit. Thus the higher-resistance circuit does not resonate as strongly and would not be as selective in a radio receiver, for example.

The figure describes a graph of current I versus frequency f. Current I r m s is plotted along Y axis and frequency f is plotted along X axis. Two curves are shown. The upper curve is for small resistance and lower curve is for large resistance. Both the curves have a smooth rise and a fall. The peaks are marked for frequency f zero. The curve for smaller resistance has a higher value of peak than the curve for large resistance.
A graph of current versus frequency for two RLC series circuits differing only in the amount of resistance. Both have a resonance at f 0 size 12{f rSub { size 8{0} } } {} , but that for the higher resistance is lower and broader. The driving AC voltage source has a fixed amplitude V 0 size 12{V rSub { size 8{0} } } {} .

Calculating resonant frequency and current

For the same RLC series circuit having a 40.0 Ω resistor, a 3.00 mH inductor, and a 5.00 μF capacitor: (a) Find the resonant frequency. (b) Calculate I rms size 12{I rSub { size 8{"rms"} } } {} at resonance if V rms size 12{V rSub { size 8{"rms"} } } {} is 120 V.

Strategy

The resonant frequency is found by using the expression in f 0 = 1 2π LC size 12{f rSub { size 8{0} } = { {1} over {2π sqrt { ital "LC"} } } } {} . The current at that frequency is the same as if the resistor alone were in the circuit.

Solution for (a)

Entering the given values for L and C into the expression given for f 0 size 12{f rSub { size 8{0} } } {} in f 0 = 1 2π LC size 12{f rSub { size 8{0} } = { {1} over {2π sqrt { ital "LC"} } } } {} yields

f 0 = 1 2π LC = 1 2π ( 3 . 00 × 10 − 3 H ) ( 5 . 00 × 10 − 6 F ) = 1 . 30 kHz . alignl { stack { size 12{f rSub { size 8{0} } = { {1} over {2π sqrt { ital "LC"} } } } {} #" "= { {1} over {2π sqrt { \( 3 "." "00" times "10" rSup { size 8{ - 3} } " H" \) \( 5 "." "00" times "10" rSup { size 8{ - 6} } " F" \) } } } =1 "." "30"" kHz" {} } } {}

Discussion for (a)

We see that the resonant frequency is between 60.0 Hz and 10.0 kHz, the two frequencies chosen in earlier examples. This was to be expected, since the capacitor dominated at the low frequency and the inductor dominated at the high frequency. Their effects are the same at this intermediate frequency.

Solution for (b)

The current is given by Ohm’s law. At resonance, the two reactances are equal and cancel, so that the impedance equals the resistance alone. Thus,

I rms = V rms Z = 120 V 40 . 0 Ω = 3 . 00 A. size 12{I rSub { size 8{"rms"} } = { {V rSub { size 8{"rms"} } } over {Z} } = { {"120"" V"} over {"40" "." "0 " %OMEGA } } =3 "." "00"" A"} {}

Discussion for (b)

At resonance, the current is greater than at the higher and lower frequencies considered for the same circuit in the preceding example.

Got questions? Get instant answers now!

Power in RLC Series ac circuits

If current varies with frequency in an RLC circuit, then the power delivered to it also varies with frequency. But the average power is not simply current times voltage, as it is in purely resistive circuits. As was seen in [link] , voltage and current are out of phase in an RLC circuit. There is a phase angle     ϕ size 12{ϕ} {} between the source voltage V size 12{V} {} and the current I size 12{I} {} , which can be found from

cos ϕ = R Z . size 12{"cos"ϕ= { {R} over {Z} } } {}

For example, at the resonant frequency or in a purely resistive circuit Z = R size 12{Z=R} {} , so that cos ϕ = 1 size 12{"cos"ϕ=1} {} . This implies that ϕ = 0 º size 12{ϕ=0 rSup { size 8{ circ } } } {} and that voltage and current are in phase, as expected for resistors. At other frequencies, average power is less than at resonance. This is both because voltage and current are out of phase and because I rms size 12{I rSub { size 8{"rms"} } } {} is lower. The fact that source voltage and current are out of phase affects the power delivered to the circuit. It can be shown that the average power is

Questions & Answers

Why is b in the answer
Dahsolar Reply
how do you work it out?
Brad Reply
answer
Ernest
heheheehe
Nitin
(Pcos∅+qsin∅)/(pcos∅-psin∅)
John Reply
how to do that?
Rosemary Reply
what is it about?
Amoah
how to answer the activity
Chabelita Reply
how to solve the activity
Chabelita
solve for X,,4^X-6(2^)-16=0
Alieu Reply
x4xminus 2
Lominate
sobhan Singh jina uniwarcity tignomatry ka long answers tile questions
harish Reply
t he silly nut company makes two mixtures of nuts: mixture a and mixture b. a pound of mixture a contains 12 oz of peanuts, 3 oz of almonds and 1 oz of cashews and sells for $4. a pound of mixture b contains 12 oz of peanuts, 2 oz of almonds and 2 oz of cashews and sells for $5. the company has 1080
ZAHRO Reply
If  , , are the roots of the equation 3 2 0, x px qx r     Find the value of 1  .
Swetha Reply
Parts of a pole were painted red, blue and yellow. 3/5 of the pole was red and 7/8 was painted blue. What part was painted yellow?
Patrick Reply
Parts of the pole was painted red, blue and yellow. 3 /5 of the pole was red and 7 /8 was painted blue. What part was painted yellow?
Patrick
how I can simplify algebraic expressions
Katleho Reply
Lairene and Mae are joking that their combined ages equal Sam’s age. If Lairene is twice Mae’s age and Sam is 69 yrs old, what are Lairene’s and Mae’s ages?
Mary Reply
23yrs
Yeboah
lairenea's age is 23yrs
ACKA
hy
Katleho
Ello everyone
Katleho
Laurene is 46 yrs and Mae is 23 is
Solomon
hey people
christopher
age does not matter
christopher
solve for X, 4^x-6(2*)-16=0
Alieu
prove`x^3-3x-2cosA=0 (-π<A<=π
Mayank Reply
create a lesson plan about this lesson
Rose Reply
Excusme but what are you wrot?
Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College physics. OpenStax CNX. Jul 27, 2015 Download for free at http://legacy.cnx.org/content/col11406/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics' conversation and receive update notifications?

Ask