| << Chapter < Page | Chapter >> Page > |
The COM of the L-shaped rod is :
and similarly,
It is important to note that the expressions of COM are independent of mass term.
Problem : A thin rod of length 3 m is bent at right angles at a distance 1 m from one end. If 1 m segment lies horizontally, determine the COM of the resulting L-shaped wire structure.
Solution : Here = 1m and = 2 m. The COM of the L - shaped rod is :
and
A semicircular wire is not symmetric to all the axes of the coordinates. The wire is a planar body involving two dimensions (x and y). However, we note that the wire is symmetric about y-axis, but not about x-axis. This has two important implications :
Thus, we need to evalute the expression :
Evaluation of an integral is based on identifying the differential element. The semicircular wire is composed of large numbers of particle like elements, each of mass "ⅆm". The idea of this particle like element of mass "dm" is that its center of mass i.e COM lies at "y" distance from the origin in y-direction. This element is linked to the mass "m" of the wire as :
Semicircular uniform wire
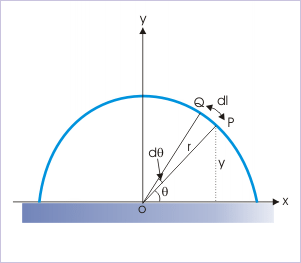
Now,
Putting in the integral,
Integrating between θ = 0 and θ = π,
The COM of the semicircular wire is ( ).
A semicircular disc is not symmetric to all the axes of the coordinates. The thin disc is a planar body involving two dimensions (x and y). However, we note that the disc is symmetric about y-axis, but not about x-axis. This has two important implications :
Thus, we need to evaluate the expression :
Evaluation of an integral is based on identifying the differential element. The semicircular disc is composed of large numbers of semicircular thin wires. We must be careful in evaluating this integral. The elemental mass "dm" corresponds to a semicirular wire - not a particle as the case before. The term "y" in the integral denotes the distance of the COM of this elemental semicircular wire. The COM of this semi-circular thin wire element is at a distance 2r/Π (as determined earlier)in y-direction.
Semicircular uniform disc
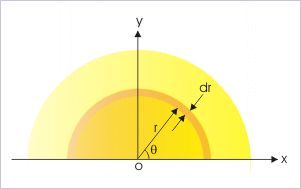
Now,
where "σ" denoted the surface density. It is given by :
Putting in the integral,
Integrating between r = 0 and r = R (radius of the semicircular disc),
The COM of the semicircular disc is ( ).
Evaluation of integrals to determine COM of non-uniform rigid bodies may be cumbersome. There are two possibilities :
If the variation in density is distinctly marked, then it is possible to determine COMs of individual uniform parts. Once COMs of the individual uniform parts are known, we can treat them as particle with their mass at their respective COMs. Thus, non-uniform rigid body is reduced to a system of particles, which renders easily for determination of its COM. This technique is illustrated in the example given here :
Problem : A thin plate (axb) is made up of two equal portions of different surface density of and as shown in the figure. Determine COM of the composite plate in the coordinate system shown.
Composite system of rigid bodies
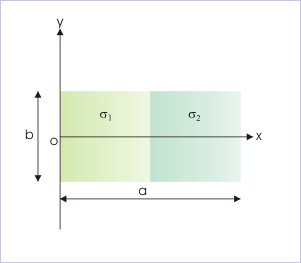
Solution : COM of the first half is at , whereas COM of the second half is at from the origin of the coordinate system in x-direction. As x-axis lies at mid point of the height of the plate, y-component of COM is zero. Now two portions are like two particles having masses :
and
Also, the x-coordinates of the positions of these particles are and . The x-component of the COM of two particles system is :
If the variation in density is well defined, then it is possible to evaluate integral to determine the COM for non-uniform rigid body. The technique is illustrated in the example given here :
Problem : Linear density of a rod varies with length as γ = 2x + 3. If the length of the rod is "L", then find the COM of the rod.
Solution : The COM of the rod in one dimension is given as :
Com of a rod with varying density
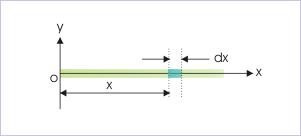
Here,
We can use this relation to determine COM as :
Evaluating between x = 0 and x = L, we have :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?