| << Chapter < Page | Chapter >> Page > |
Theorem of perpendicular axes is applicable to planar bodies only. According to this theorem, moment of inertia of a planar rigid body about a perpendicular axis (z) is equal to the sum of moments of inertia about two mutually perpendicular axes (x and y) in the plane of the body, which are themselves perpendicular to the z - axis.
Theorem of perpendicular axes
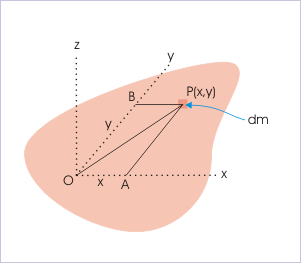
Three axes involved in the theorem are mutually perpendicular to each other and form the rectangular coordinate system. It should be noted that there is no restriction that axes pass through center of mass of the rigid body as in the case of parallel axis theorem. In order to prove the theorem in general, we consider a planar body of irregular shape. We consider an elemental mass "dm" at P (x,y) as shown in the figure above.
The moment of inertia of the body about z - axis is given as :
We drop two perpendiculars in the plane of body on "x" and "y" axes. Then,
Substituting in the equation of moment of inertia,
The expressions on the right hand side represent moments of inertia of the body about "x" and "y" axes. Hence,
We shall determine MIs of objects about other axes, which are not symmetric to the body. As pointed out earlier, we shall limit the application of the theorem of perpendicular axes to planar objects like rectangular plate, ring and circular plate etc.
(i) Rectangular plate : about a line passing through center of mass and perpendicular to the plane
Moment of inertia about a line passing through center of mass and parallel to one of the side is given as :
Theorem of perpendicular axes
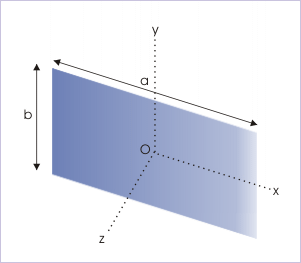
Applying theorem of perpendicular axes, we have :
(ii) Circular ring : about one of the diameter
Moment of inertia about a perpendicular line passing through center of ring is given as :
Theorem of perpendicular axes
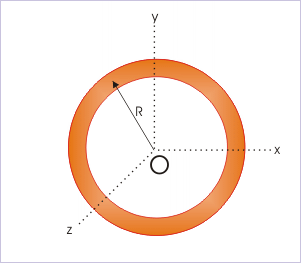
We consider two mutually perpendicular diameters as "x" and "y" axes of the cordinate system. Now, applying theorem of perpendicular axes, we have :
However, the circular ring has uniform mass distribution, which is symmetrically distributed about any diameter. Thus, MIs about the axes "x" and "y" are equal,
Thus,
(iii) Circular plate : about one of the diameter
Moment of inertia about a perpendicular line passing through center of circular plate is given as :
Theorem of perpendicular axes
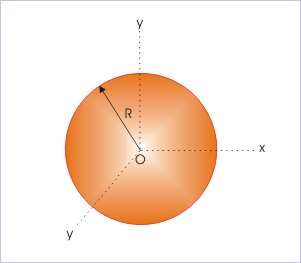
We consider two mutually perpendicular diameters as shown in the figure. These diameters can be treated as two coordinates of the plane of the circular plate. Now, applying theorem of perpendicular axes, we have :
However, the circular plate has uniform mass distribution, which is symmetrically distributed about any diameter. Thus, MIs about the planar axes "x" and "y" are equal,
Thus,
1. Theorem of perpendicular axes
The mathematical expression of this theorem is given as :
where is MI of the body about an axis passing through center of mass, "C"; I is MI of the body about an axis parallel to the axis passing through center of mass; "M" is the mass of the rigid body and "d" is the perpendicular distance between two parallel axes.
2. Theorem of parallel axes is valid for all shapes (regular and irregular).
3. Theorem of parallel axes expresses MI about a parallel axis in terms of the MI about a parallel axis passing through COM. Thus, we should ensure that one of the two parallel axes be through the COM of the rigid body.
4. Theorem of perpendicular axes
According to this theorem, moment of inertia of a planar rigid body about a perpendicular axis (z) is equal to the sum of moments of inertia about two mutually perpendicular axes (x and y) in the plane of the body, which are also perpendicular to the axis along z - axis.
4. Theorem of perpendicular axes is valid only for all planar shapes (regular and irregular).

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?