| << Chapter < Page | Chapter >> Page > |
Theorem of parallel axes
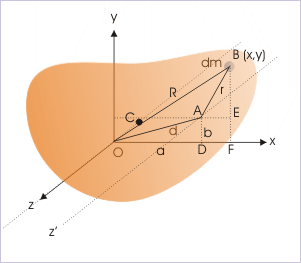
Now, MI of the rigid body about axis Az' in the form of integral is given by :
Rearranging, we have :
However, the coordinates of the center of mass by definition are given as :
But, we see here that "x" and "y" coordinates of center of mass are zero as it lies on z - axis. It means that :
Similarly,
Thus, the equation for the MI of the rigid body about the axis parallel to an axis passing through center of mass "C" is :
From the figure,
and
Substituting in the equation of MI, we have :
We, however, note that "R" is variable, but "d" is constant. Taking the constant out of the integral sign :
The integral on right hand side is the expression of MI of the rigid body about the axis passing through center of mass. Hence,
We shall illustrate application of the theorem of parallel axes to some of the regular rigid bodies, whose MI about an axis passing through center of mass is known.
(i) Rod : about an axis perpendicular to the rod and passing through one of its ends
Theorem of parallel axes
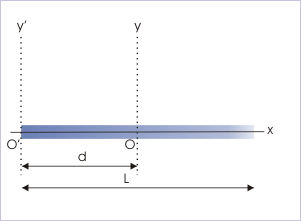
MI about perpendicular bisector is known and is given by :
According to theorem of parallel axes,
(ii) Circular ring : about a line tangential to the ring
Theorem of parallel axes
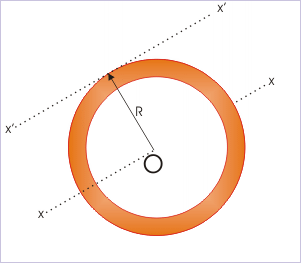
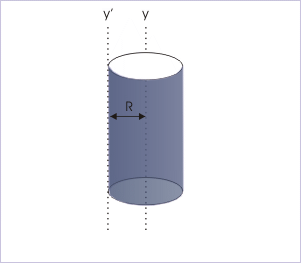
MI about an axis passing through the center and perpendicular to the ring is known and is given by :
According to theorem of parallel axes,
Since hollow cylinder has similar expression of MI, the expression for the MI about a line tangential to its curved surface is also same.
(i) Circular plate : about a line perpendicular and tangential to the circular plate
Theorem of parallel axes


MI about an axis passing through the center and perpendicular to the circular plate is known and is given by :
According to theorem of parallel axes,
Since solid cylinder has similar expression of MI, the expression for the MI about a line tangential to its curved surface is also same.
(iii) Hollow sphere : about a line tangential to the hollow sphere
Theorem of parallel axes
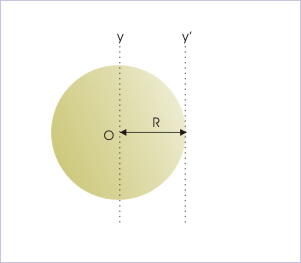
MI about one of its diameters is known and is given by :
According to theorem of parallel axes,
(iv) Solid sphere : about a line tangential to the solid sphere
Theorem of parallel axes

MI about one of its diameters is known and is given by :
According to theorem of parallel axes,

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?