| << Chapter < Page | Chapter >> Page > |
Solution : We shall work out MI from the basic integral expression for elemental mass :
Let us consider an small element "dx" along the length, which is situated at a linear distance "x" from the axis. The elemental mass, however, is at a perpendicular distance AB from the axis of rotation – not “x’.
Mi of a rod
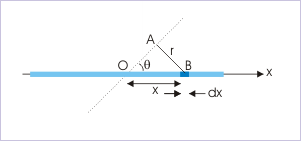
From ΔOAB,
The above expression allows us to convert all distances involved in the calculation of MI in terms of a single variable "x". Now, the elemental mass (dm) is, given as :
The MI of elemental mass about inclined axis AA' is :
The MI of rod about inclined axis AA', therefore, is :
We note here that the angle "θ" is constant for all elemental masses along the rod and, thus " " together with "M/L" can be taken out of the integral sign. The appropriate limits of integration covering the length of the rod are "-L/2" and "L/2" :
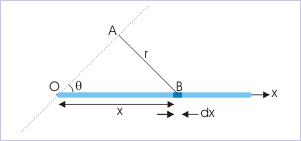
Note1 : Here, is MI of the rod about perpendicular line through COM, denoted by Ic. The moment of inertia about an axis making an angle with the rod, therefore, can be expressed in terms of "Ic" as :
Note2 : The MI of the rod at an inclined axis passing through one of its edge is obtained by integrating between limits "0" and "L" :
Mi of a rod
Example 6
Problem : The mass per unit length of a non-uniform rod of mass “M” and length “L” is given as “ax”, where “x” is measured from left end and “a” is a constant. What is its moment of inertia about an axis perpendicular to the rod and passing through its left end ( point “O”) ?
Mi of a rod
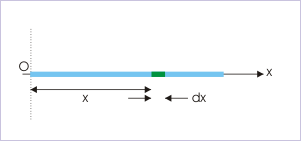
Solution : Let us now consider a small length “dx” at a distance “x” from the axis of rotation. The elemental mass is,
In order to evaluate the constant “a”, we integrate the elemental mass for the whole length of the rod and equate the same to its mass as :
Putting the appropriate limit,
Thus, elemental mass is :
The moment of inertia of the elemental mass about the axis is :
Integrating between the limits “0” and “L”, we have :
Example 7
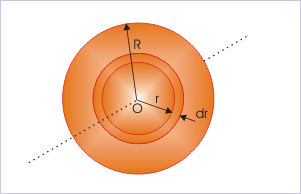
Problem : A circular disk of radius “R” and mass “M” has non-uniform surface mass density, given by , where “r” is the distance from the center of the disk and “a” is a constant. What is its MI about the perpendicular central axis ?
Solution : Let us now consider a small concentric area of thickness “dr” at a distance “r” from the axis of rotation. The elemental mass is,
Mi of a circular plate
In order to evaluate the constant “a”, we integrate the elemental mass for the whole of the circular disk and equate the same to its mass as :
Putting the appropriate limit,
Thus, elemental mass is :
The moment of inertia of the ring of elemental mass about the axis is :
Integrating between the limits “0” and “R”, we have :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?