| << Chapter < Page | Chapter >> Page > |
Questions and their answers are presented here in the module text format as if it were an extension of the treatment of the topic. The idea is to provide a verbose explanation, detailing the application of theory. Solution presented is, therefore, treated as the part of the understanding process – not merely a Q/A session. The emphasis is to enforce ideas and concepts, which can not be completely absorbed unless they are put to real time situation.
We discuss problems, which highlight certain aspects of the vector product. For this reason, questions are categorized in terms of the characterizing features of the subject matter :
Problem : Determine whether vectors 2 i – j + 2 k and 3 i – 3 j + 6 k are parallel to each other?
Solution : If the two vectors are parallel, then ratios of corresponding components of vectors in three coordinate directions are equal. Here,
The ratios are, therefore, not equal. Hence, given vectors are not parallel to each other.
Problem : Find unit vector in the direction perpendicular to vectors i + j – 2 k and 2 i – j + 3 k .
Solution : We know that cross product of two vectors is perpendicular to each of vectors. Thus, unit vector in the direction of cross product is perpendicular to the given vectors. Now, unit vector of cross product is given by :
Vector product
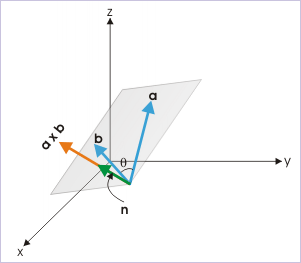
Here,
Problem : Verify vector equality B = C , if AxB = AxC .
Solution : Let and be the angles for first and second pairs of cross products. Then,
It is clear that B = C is true only when . It is always possible that the angles involved or the directions of cross products are different. Thus, we can conclude that B need not be equal to C .
Problem : If a.b = | axb | for unit vectors a and b , then find the angle between unit vectors.
Solution : According to question,
Problem : The diagonals of a parallelogram are represented by vectors 3 i + j + k and i - j - k . Find the area of parallelogram.
Solution : The area of parallelogram whose sides are formed by vectors a and b , is given by :
However, we are given in question vectors representing diagonals – not the sides. But, we know that the diagonals are sum and difference of vectors representing sides of a parallelogram. It means that :
Diagonals of a parallelogram
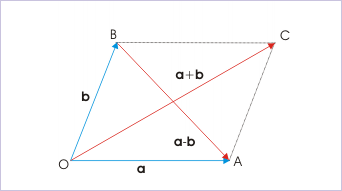
and
Now the vector product of vectors representing diagonals is :
Using anti-commutative property of vector product,
Thus,
The volume of the parallelogram is :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?