Парцијални изводи од прв ред

Нека функцијата $z=f(x_1,x_2,\text{.}\text{.}\text{.},x_n)$ е дефинирана во околина на точката $A(a_1,a_2,\text{.}\text{.}\text{.},a_n)$ .

Дефиниција.

Разликата

${\mathrm{\Delta x}}_k=x_k-a_k$

се нарекува нараснување на променливата $x_k$ , а разликата

${\Delta }_{k}f(A)=f(a_1,\text{.}\text{.}\text{.},a_k+{\mathrm{\Delta x}}_k,\text{.}\text{.}\text{.},a_n)-f(a_1,\text{.}\text{.}\text{.},a_k,\text{.}\text{.}\text{.},a_n)$

парцијално нараснување на функцијата $f$ во точката $A$ по променливата $x_k$ .

Дефиниција.

Ако постои граничната вредност

$\underset{{\mathrm{\Delta x}}_k\to 0}{\text{lim}}\frac{{\Delta }_{k}f(A)}{{\mathrm{\Delta x}}_k}=\underset{{\mathrm{\Delta x}}_k\to 0}{\text{lim}}\frac{f(a_1,\text{.}\text{.}\text{.},a_k+{\mathrm{\Delta x}}_k,\text{.}\text{.}\text{.},a_n)-f(a_1,\text{.}\text{.}\text{.},a_k,\text{.}\text{.}\text{.},a_n)}{{\mathrm{\Delta x}}_k}$

таа се нарекува парцијален извод на функцијата $f$ по променливата $x_k$ во точката $A$ и се означува со

$\frac{\partial f(A)}{\partial x_k}$ или $f_{x_k}^{\text{'}}(A)$ или $\frac{\partial z(A)}{\partial x_k}$ или $z_{x_k}^{\text{'}}$ .

Изразот $\frac{\partial f(A)}{\partial x_k}$ скратено ја означува вредноста на изводот во дадена точка $\frac{\partial f(X)}{\partial x_k}{\mid }_{X=A}$ .

За функција со две променливи $z=f(x,y)$ се дефинираат два парцијални извода, по секоја независна променлива. Нека $A(x_0,y_0)$ е точка од дефиниционата област на функцијата $f(x,y)$ и нека $\mathrm{\Delta x}$ и $\mathrm{\Delta y}$ се соодветните нараснувања на променливите $x$ и $y$ .

Дефиниција.

П арцијален извод по променливата x за фунцијата $f(x,y)$ во точката $A(x_0,y_0)$ е граничната вредност

$\underset{\mathrm{\Delta x}\to 0}{\text{lim}}\frac{f(x_0+\mathrm{\Delta x},y_0)-f(x_0,y_0)}{\mathrm{\Delta x}}=\frac{\partial f(x_0,y_0)}{\partial x}\text{.}$

Аналогно,

Дефиниција.

П арцијален извод по променливата y з а фунцијата $f(x,y)$ во точката А ( x ₀ , y ₀ ) е граничната вредност

$\underset{\mathrm{\Delta y}\to 0}{\text{lim}}\frac{f(x_0,y_0+\mathrm{\Delta y})-f(x_0,y_0)}{\mathrm{\Delta y}}=\frac{\partial f(x_0,y_0)}{\partial y}\text{.}$

Парцијалните изводи $\frac{\partial f(x_0,y_0)}{\partial x},\frac{\partial f(x_0,y_0)}{\partial y}$ на функцијата $f(x,y)$ обично се пресме­туваат во произволна точка $X(x,y)$ од дефиниционата област. Кога се бара парцијал­ниот извод по променливата $x$ , промелнливата $y$ се смета за константа и обратно.

Парцијалните изводи се означуваат со некоја од ознаките:

парцијален извод по $x$ : $f_x^{\text{'}}(x,y),f_x^{\text{'}},z_x^{\text{'}},\frac{\partial f}{\partial x},\frac{\partial z}{\partial x}$ ;

парцијален извод по $y$ : $f_y^{\text{'}}(x,y),f_y^{\text{'}},z_y^{\text{'}},\frac{\partial f}{\partial y},\frac{\partial z}{\partial y}$ .

Пример 1 . Да се најдат парцијалните изводи на функцијата $z=\text{ln}\frac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}+x}$ .

Решение . Зададената функција е функција од две независни променливи и затоа ќе има два парцијални извода по секоја променлива. Се пресметува парцијалниот извод по променливата $x$ :

$\frac{\partial z}{\partial x}=\frac{1}{\frac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}+x}}{\left(\frac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}+x}\right)}_{x^{\prime }}=$ $=\left(\frac{\sqrt{x^2+y^2}+x}{\sqrt{x^2+y^2}-x}\right)\cdot \frac{\left(\frac{x}{\sqrt{x^2+y^2}}-1\right)\left(\sqrt{x^2+y^2}+x\right)-\left(\sqrt{x^2+y^2}-x\right)\left(\frac{x}{\sqrt{x^2+y^2}}+1\right)}{{\left(\sqrt{x^2+y^2}+x\right)}^2}=$

$=\left(\frac{\sqrt{x^2+y^2}+x}{\sqrt{x^2+y^2}-x}\right)\cdot \frac{\frac{\left(x-\sqrt{x^2+y^2}\right)\left(\sqrt{x^2+y^2}+x\right)-\left(\sqrt{x^2+y^2}-x\right)\left(x+\sqrt{x^2+y^2}\right)}{\sqrt{x^2+y^2}}}{{\left(\sqrt{x^2+y^2}+x\right)}^2}=$ $$

$=\left(\frac{\sqrt{x^2+y^2}+x}{\sqrt{x^2+y^2}-x}\right)\cdot \frac{x^2-x^2-y^2-\left(x^2+y^2-x^2\right)}{\sqrt{x^2+y^2}{\left(\sqrt{x^2+y^2}+x\right)}^2}=$

$=\frac{-{\mathrm{2y}}^2}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)\left(\sqrt{x^2+y^2}+x\right)}=$ $=\frac{-{\mathrm{2y}}^2}{\sqrt{x^2+y^2}\left(x^2+y^2-x^2\right)}=\frac{-{\mathrm{2y}}^2}{y^2\sqrt{x^2+y^2}}=\frac{-2}{\sqrt{x^2+y^2}}$ ,

од каде следува дека $$ $\frac{\partial z}{\partial x}=\frac{-2}{\sqrt{x^2+y^2}}$ .

Сега се пресметува и парцијалниот извод по променливата $y$ :

$\frac{\partial z}{\partial y}=\frac{1}{\frac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}+x}}{\left(\frac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}+x}\right)}_{y^{\prime }}=\left(\frac{\sqrt{x^2+y^2}+x}{\sqrt{x^2+y^2}-x}\right)\cdot \frac{\frac{y}{\sqrt{x^2+y^2}}\left(\sqrt{x^2+y^2}+x\right)-\left(\sqrt{x^2+y^2}-x\right)\frac{y}{\sqrt{x^2+y^2}}}{{\left(\sqrt{x^2+y^2}+x\right)}^2}=$

$=\left(\frac{\sqrt{x^2+y^2}+x}{\sqrt{x^2+y^2}-x}\right)\cdot \frac{y\left(\sqrt{x^2+y^2}+x\right)-y\left(\sqrt{x^2+y^2}-x\right)}{\sqrt{x^2+y^2}{\left(\sqrt{x^2+y^2}+x\right)}^2}=$

$=\frac{y\left(\sqrt{x^2+y^2}+x-\sqrt{x^2+y^2}-x\right)}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)\left(\sqrt{x^2+y^2}+x\right)}=$ $\frac{2\text{xy}}{\sqrt{x^2+y^2}\left(x^2+y^2-x^2\right)}=\frac{2\text{xy}}{y^2\sqrt{x^2+y^2}}=\frac{\mathrm{2x}}{y\sqrt{x^2+y^2}}$ ,

и се добива $\frac{\partial z}{\partial y}=\frac{\mathrm{2x}}{y\sqrt{x^2+y^2}}$ . ◄

Од важност се следните тврдења:

• ( Потребни услови за диференцијабилност ) Ако функција $z=f(x,y)$ е диференцијабилна во дадена точка, тогаш постојат сите парцијални изводи во таа точка.

• ( Доволен услов за диференцијабилност ) Ако функција $z=f(x,y)$ во околина на дадена точка има непрекинати парцијални изводи по секоја променлива, тогаш таа е диференцијабилна во таа точка.

• Ако функцијата $z=f(x,y)$ е диференцијабилна во дадена точка, тогаш таа е непрекината во таа точка.

Геометриско толкување на парцијалнте изводи на функција од две променливи

Нека го разгледуваме делот од графикот на диферен­цијабилната функција $z=f(x,y)$ во точката $A(x_0,y_0)\in D_f$ . Ако во функцијата $f(x,y)$ променливата $y$ се фиксира со константна вредност $y_0$ , тогаш таа се смета за функција со една променлива $x$ , односно $\varphi (x)=f(x,y_0)$ , а нејзиниот график претставува крива која се добива како пресек на разгледуваниот дел од површината и рамнината $y=\text{const}=y_0$ .

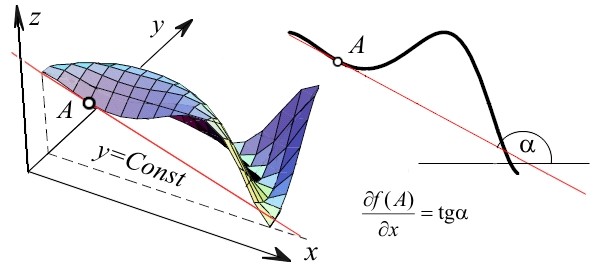Слика 1. Геометриско толкување на парцијалниот извод по x

Наклонот на тангентата tg $\alpha$ на оваа крива во точката $A$ во однос на позитивната насока на $x-$ оската е парцијалниот извод (Сл. 1) $f_x^{\text{'}}(A)=\frac{\partial f(A)}{\partial x}=\text{tg}\alpha \text{.}$

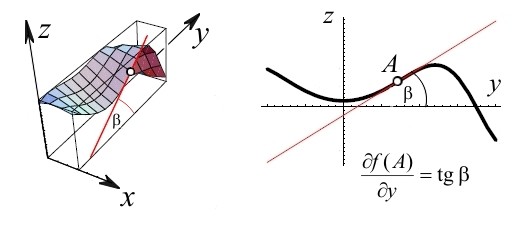Слика 2. Геометриско толкување на парцијалниот извод по $y$

Аналогно, со фиксирање на $x=x_0$ , функцијата $z=f(x,y)$ се сведува на функција со една променлива $y$ , односно $\psi (y)=f(x_0,y)$ , а наклонот на тангентата на оваа крива која лежи во рамнината $x=x_0$ е парцијалниот извод (Сл. 2) $f_y^{\text{'}}(A)=\frac{\partial f(A)}{\partial y}=\text{tg}\beta \text{.}$