This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr.
The symbols, notations, and properties of numbers that form the basis of algebra, as well as exponents and the rules of exponents, are introduced in this chapter. Each property of real numbers and the rules of exponents are expressed both symbolically and literally. Literal explanations are included because symbolic explanations alone may be difficult for a student to interpret.Objectives of this module: understand the power rules for powers, products, and quotients.
Overview
- The Power Rule for Powers
- The Power Rule for Products
- The Power Rule for quotients
The power rule for powers
The following examples suggest a rule for raising a power to a power:
Using the product rule we get
Power rule for powers
If
is a real number and
and
are natural numbers,
To raise a power to a power, multiply the exponents.
Sample set a
Simplify each expression using the power rule for powers. All exponents are natural numbers.
Although we don’t know exactly what number
is, the notation
indicates the multiplication.
Practice set a
Simplify each expression using the power rule for powers.
The power rule for products
The following examples suggest a rule for raising a product to a power:
Power rule for products
If
and
are real numbers and
is a natural number,
To raise a product to a power, apply the exponent to each and every factor.
Sample set b
Make use of either or both the power rule for products and power rule for powers to simplify each expression.
Practice set b
Make use of either or both the power rule for products and the power rule for powers to simplify each expression.
The power rule for quotients
The following example suggests a rule for raising a quotient to a power.
Power rule for quotients
If
and
are real numbers and
is a natural number,
To raise a quotient to a power, distribute the exponent to both the numerator and denominator.
Sample set c
Make use of the power rule for quotients, the power rule for products, the power rule for powers, or a combination of these rules to simplify each expression. All exponents are natural numbers.
Practice set c
Make use of the power rule for quotients, the power rule for products, the power rule for powers, or a combination of these rules to simplify each expression.
Exercises
Use the power rules for exponents to simplify the following problems. Assume that all bases are nonzero and that all variable exponents are natural numbers.
Exercises for review
(
[link] ) Is there a smallest integer? If so, what is it?
(
[link] ) Use the distributive property to expand
.
(
[link] ) Find the value of
.
(
[link] ) Assuming the bases are not zero, find the value of
.
(
[link] ) Assuming the bases are not zero, find the value of
.
![]()
![]()
![]()
![]()
![]()
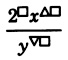
![]()
