| << Chapter < Page | Chapter >> Page > |
In this section, we examine Green’s theorem, which is an extension of the Fundamental Theorem of Calculus to two dimensions. Green’s theorem has two forms: a circulation form and a flux form, both of which require region D in the double integral to be simply connected. However, we will extend Green’s theorem to regions that are not simply connected.
Put simply, Green’s theorem relates a line integral around a simply closed plane curve C and a double integral over the region enclosed by C . The theorem is useful because it allows us to translate difficult line integrals into more simple double integrals, or difficult double integrals into more simple line integrals.
Recall that the Fundamental Theorem of Calculus says that
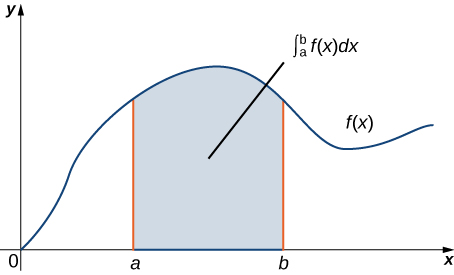
As a geometric statement, this equation says that the integral over the region below the graph of and above the line segment depends only on the value of F at the endpoints a and b of that segment. Since the numbers a and b are the boundary of the line segment the theorem says we can calculate integral based on information about the boundary of line segment ( [link] ). The same idea is true of the Fundamental Theorem for Line Integrals:
When we have a potential function (an “antiderivative”), we can calculate the line integral based solely on information about the boundary of curve C .
Green’s theorem takes this idea and extends it to calculating double integrals. Green’s theorem says that we can calculate a double integral over region D based solely on information about the boundary of D . Green’s theorem also says we can calculate a line integral over a simple closed curve C based solely on information about the region that C encloses. In particular, Green’s theorem connects a double integral over region D to a line integral around the boundary of D .
The first form of Green’s theorem that we examine is the circulation form. This form of the theorem relates the vector line integral over a simple, closed plane curve C to a double integral over the region enclosed by C . Therefore, the circulation of a vector field along a simple closed curve can be transformed into a double integral and vice versa.
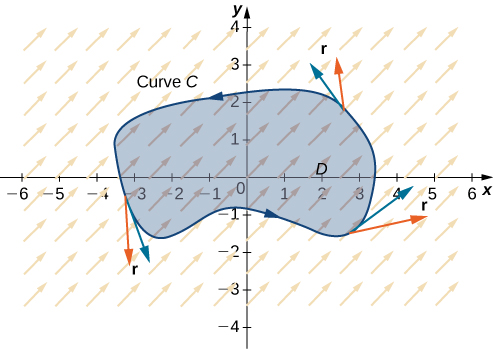
Let D be an open, simply connected region with a boundary curve C that is a piecewise smooth, simple closed curve oriented counterclockwise ( [link] ). Let be a vector field with component functions that have continuous partial derivatives on D . Then,
Notice that Green’s theorem can be used only for a two-dimensional vector field F . If F is a three-dimensional field, then Green’s theorem does not apply. Since

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?