| << Chapter < Page | Chapter >> Page > |
Shannon's Source Coding Theorem has additional applications in data compression . Here, we have a symbolic-valued signal source, like a computer file or an image, that we want torepresent with as few bits as possible. Compression schemes that assign symbols to bit sequences are known as lossless if they obey the Source Coding Theorem; they are lossy if they use fewer bits than the alphabet's entropy. Using a lossy compression scheme means that you cannotrecover a symbolic-valued signal from its compressed version without incurring some error. You might be wondering why anyonewould want to intentionally create errors, but lossy compression schemes are frequently used where the efficiency gained inrepresenting the signal outweighs the significance of the errors.
Shannon's Source Coding Theorem states that symbolic-valued signals require on the average at least number of bits to represent each of its values, which aresymbols drawn from the alphabet . In the module on the Source Coding Theorem we find that using a so-called fixed rate source coder, one that produces a fixed number of bits/symbol, may not be the most efficient way of encodingsymbols into bits. What is not discussed there is a procedure for designing an efficient source coder: one guaranteed to produce the fewest bits/symbol on the average. That source coder is not unique,and one approach that does achieve that limit is the Huffman source coding algorithm .
The simple four-symbol alphabet used in the Entropy and Source Coding modules has a four-symbol alphabet with the following probabilities, and an entropy of 1.75 bits . This alphabet has the Huffman coding tree shown in [link] .
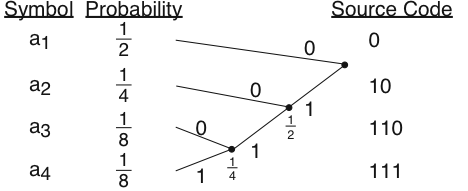
The code thus obtained is not unique as we could have labeled the branches coming out of each node differently. The averagenumber of bits required to represent this alphabet equals bits, which is the Shannon entropy limit for this source alphabet. If we had thesymbolic-valued signal , our Huffman code would produce the bitstream .
If the alphabet probabilities were different, clearly a different tree, and therefore different code, could wellresult. Furthermore, we may not be able to achieve the entropy limit. If our symbols had the probabilities , , , and , the average number of bits/symbol resulting from the Huffman coding algorithm would equal bits. However, the entropy limit is 1.68 bits. The Huffman code does satisfy the SourceCoding Theorem—its average length is within one bit of the alphabet's entropy—but you might wonder if a better codeexisted. David Huffman showed mathematically that no other code could achieve a shorter average code than his. We can'tdo better.
Derive the Huffman code for this second set of probabilities, and verify the claimed average code lengthand alphabet entropy.
The Huffman coding tree for the second set of probabilities is identical to that for the first ( [link] ). The average code length is bits. The entropy calculation is straightforward: , which equals bits.

Notification Switch
Would you like to follow the 'Fundamentals of electrical engineering i' conversation and receive update notifications?