6.2 Line integrals  (Page 3/20)

Note that in a scalar line integral, the integration is done with respect to arc length s , which can make a scalar line integral difficult to calculate. To make the calculations easier, we can translate ${\displaystyle {\int }_{C}fds}$ to an integral with a variable of integration that is t .

Let $\text{r}\left(t\right)=⟨x\left(t\right),y\left(t\right),z\left(t\right)⟩$ for $a\le t\le b$ be a parameterization of $C.$ Since we are assuming that $C$ is smooth, $r^{\prime }\left(t\right)=⟨x^{\prime }\left(t\right),y^{\prime }\left(t\right),z^{\prime }\left(t\right)⟩$ is continuous for all $t$ in $\left[a,b\right].$ In particular, $x\text{′}\left(t\right),y\text{′}\left(t\right),$ and $z\text{′}\left(t\right)$ exist for all $t$ in $\left[a,b\right].$ According to the arc length formula, we have

If width $\text{Δ}{t}_i=t_i-t_{i-1}$ is small, then function ${\displaystyle {\int }_{t_{i-1}}^{t_i}\Vert r^{\prime }\left(t\right)\Vert dt\approx \Vert r^{\prime }\left(t_i^{*}\right)\Vert \text{Δ}{t}_i,}$ $\Vert r^{\prime }\left(t\right)\Vert$ is almost constant over the interval $\left[t_{i-1},t_i\right].$ Therefore,

and we have

See [link] .

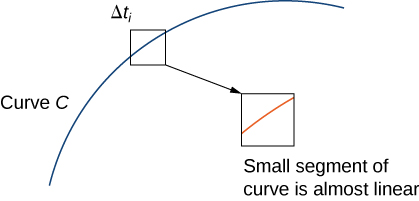
Note that

In other words, as the widths of intervals $[t_{i-1},t_i]$ shrink to zero, the sum ${\displaystyle \sum _{i=1}^{n}f(\text{r}(t_i^{*}))}\Vert r^{\prime }(t_i^{*})\Vert \text{Δ}{t}_i$ converges to the integral ${\displaystyle {\int }_a^{b}f(\text{r}(t))}\Vert r^{\prime }(t)\Vert dt.$ Therefore, we have the following theorem.

Although we have labeled [link] as an equation, it is more accurately considered an approximation because we can show that the left-hand side of [link] approaches the right-hand side as $n\to \infty .$ In other words, letting the widths of the pieces shrink to zero makes the right-hand sum arbitrarily close to the left-hand sum. Since

we obtain the following theorem, which we use to compute scalar line integrals.

Note that a consequence of this theorem is the equation $ds=\Vert r^{\prime }\left(t\right)\Vert dt.$ In other words, the change in arc length can be viewed as a change in the t domain, scaled by the magnitude of vector $r^{\prime }\left(t\right).$