1. Home
  2. Calculus volume 2
  3. Sequences and series
  4. Alternating series

5.5 Alternating series

<< Chapter < Page
  Calculus volume 2     Page 1 / 10
Chapter >> Page >
  • Use the alternating series test to test an alternating series for convergence.
  • Estimate the sum of an alternating series.
  • Explain the meaning of absolute convergence and conditional convergence.

So far in this chapter, we have primarily discussed series with positive terms. In this section we introduce alternating series—those series whose terms alternate in sign. We will show in a later chapter that these series often arise when studying power series. After defining alternating series, we introduce the alternating series test to determine whether such a series converges.

The alternating series test

A series whose terms alternate between positive and negative values is an alternating series    . For example, the series

∑ n = 1 ∞ ( − 1 2 ) n = − 1 2 + 1 4 − 1 8 + 1 16 − ⋯

and

∑ n = 1 ∞ ( −1 ) n + 1 n = 1 − 1 2 + 1 3 − 1 4 + ⋯

are both alternating series.

Definition

Any series whose terms alternate between positive and negative values is called an alternating series. An alternating series can be written in the form

∑ n = 1 ∞ ( −1 ) n + 1 b n = b 1 − b 2 + b 3 − b 4 + ⋯

or

∑ n − 1 ∞ ( −1 ) n b n = − b 1 + b 2 − b 3 + b 4 − ⋯

Where b n ≥ 0 for all positive integers n .

Series (1), shown in [link] , is a geometric series. Since | r | = | − 1 / 2 | < 1 , the series converges. Series (2), shown in [link] , is called the alternating harmonic series. We will show that whereas the harmonic series diverges, the alternating harmonic series converges.

To prove this, we look at the sequence of partial sums { S k } ( [link] ).

Proof

Consider the odd terms S 2 k + 1 for k ≥ 0 . Since 1 / ( 2 k + 1 ) < 1 / 2 k ,

S 2 k + 1 = S 2 k − 1 − 1 2 k + 1 2 k + 1 < S 2 k − 1 .

Therefore, { S 2 k + 1 } is a decreasing sequence. Also,

S 2 k + 1 = ( 1 − 1 2 ) + ( 1 3 − 1 4 ) + ⋯ + ( 1 2 k − 1 − 1 2 k ) + 1 2 k + 1 > 0 .

Therefore, { S 2 k + 1 } is bounded below. Since { S 2 k + 1 } is a decreasing sequence that is bounded below, by the Monotone Convergence Theorem, { S 2 k + 1 } converges. Similarly, the even terms { S 2 k } form an increasing sequence that is bounded above because

S 2 k = S 2 k − 2 + 1 2 k − 1 − 1 2 k > S 2 k − 2

and

S 2 k = 1 + ( − 1 2 + 1 3 ) + ⋯ + ( − 1 2 k − 2 + 1 2 k − 1 ) − 1 2 k < 1 .

Therefore, by the Monotone Convergence Theorem, the sequence { S 2 k } also converges. Since

S 2 k + 1 = S 2 k + 1 2 k + 1 ,

we know that

lim k → ∞ S 2 k + 1 = lim k → ∞ S 2 k + lim k → ∞ 1 2 k + 1 .

Letting S = lim k → ∞ S 2 k + 1 and using the fact that 1 / ( 2 k + 1 ) → 0 , we conclude that lim k → ∞ S 2 k = S . Since the odd terms and the even terms in the sequence of partial sums converge to the same limit S , it can be shown that the sequence of partial sums converges to S , and therefore the alternating harmonic series converges to S .

It can also be shown that S = ln 2 , and we can write

∑ n = 1 ∞ ( −1 ) n + 1 n = 1 − 1 2 + 1 3 − 1 4 + ⋯ = ln ( 2 ) .
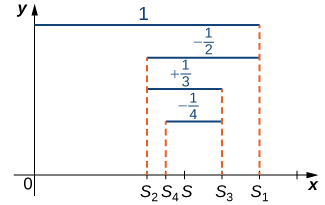
This graph demonstrates the alternating hamanic series in the first quadrant. The highest line 1 is drawn to S1, the next line -1/2 is drawn to S2, the next line +1/3 is drawn to S3, the line -1/4 is drawn to S4, and the last line +1/5 is drawn to S5. The odd terms are decreasing and bounded below, and the even terms are increasing and bounded above. It seems to be converging to S, which is in the middle of S2, S4 and S5, S3, S1.
For the alternating harmonic series, the odd terms S 2 k + 1 in the sequence of partial sums are decreasing and bounded below. The even terms S 2 k are increasing and bounded above.

□

More generally, any alternating series of form (3) ( [link] ) or (4) ( [link] ) converges as long as b 1 ≥ b 2 ≥ b 3 ≥ ⋯ and b n → 0 ( [link] ). The proof is similar to the proof for the alternating harmonic series.

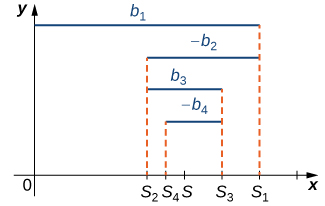
This diagram illustrates an alternating series in quadrant 1. The highest line b1 is drawn out to S1, the next line –b2 is drawn back to S2, the next line b3 is drawn out to S3, the next line –b4 is drawn back to S4, and the last line is drawn out to S5. It seems to be converging to S, which is in between S2, S4 and S5, S3, and S1. The odd terms are decreasing and bounded below. The even terms are increasing and bounded above.
For an alternating series b 1 − b 2 + b 3 − ⋯ in which b 1 > b 2 > b 3 > ⋯ , the odd terms S 2 k + 1 in the sequence of partial sums are decreasing and bounded below. The even terms S 2 k are increasing and bounded above.

Alternating series test

An alternating series of the form

∑ n = 1 ∞ ( −1 ) n + 1 b n or ∑ n = 1 ∞ ( −1 ) n b n

converges if

  1. 0 ≤ b n + 1 ≤ b n for all n ≥ 1 and
  2. lim n → ∞ b n = 0 .

This is known as the alternating series test    .
<< Chapter < Page Page > Chapter >>
Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 2. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11965/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?

Ask