| << Chapter < Page | Chapter >> Page > |
Idea of "continuity" in the context of function is same as its dictionary meaning. It simply means that function is continuous without any abrupt or sudden change in the value of function. An indicative way to test continuity is to see (graphically or otherwise) that there is no sudden jump in function value in the domain of function. If domain of function is a continuous interval i.e. no points or sub-intervals are excluded from real number set representing domain, then we can draw a continuous function without lifting the drawing instrument i.e. pen, pencil etc. If we have to lift the pen in order to complete the graph of a function in the continuous interval, then function is not continuous.
The feature of continuity is related to function. Therefore, continuity of a function is meaningful in its domain only. It means that we do not need to evaluate continuity in intervals or points where function is not defined. This is an important consideration that helps us to differentiate between “discontinuity” and “undefined values”.
The condition of continuity is expressed in terms of limit and function value. Both of these are required to exist and be equal. We shall learn about these aspects more in detail after having brief overview of these terms.
The limit from left means that a function approaches a value ( ) as x approaches the test point “a” from left such that x is always less than “a” – but not equal to “a”.
We show here three illustrations of “limit from left”. The important aspect of these figures is that graph tends to a particular value (infinity is also included). This is done by showing the orientation of graph pointing to limiting value when x is infinitesimally close to test point. Important point to note is that graph does not reach limiting value. Note empty circle at the end of graph, which represents the value of limit not yet occupied by graph. Similarly, asymptotic nature of graph tending to infinity maintains a small distance away from asymptotes, denoting that graph does not reach limiting value.
Limit from left
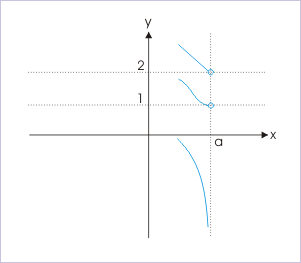
The limit from right means that a function approaches a value ( ) as x approaches the test point “a” from right such that x is always greater than “a” – but not equal to “a”.
We show here three illustrations of “limit from right" as in the earlier case. Important point to note is that graph does not reach limiting value, which represents the value of limit not yet occupied by graph.
Limit from right
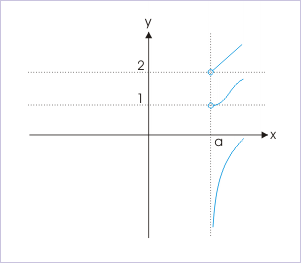
The limit at a point means that a function approaches a value (L) as x approaches the test point “a” from either side.
We show here three illustrations of limit at a point. Important point to again note is that graph does not reach limiting value, which represents the value of limit not yet occupied by graph.
Limit at a point
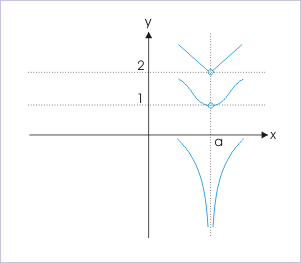
Function value is obtained by substituting x values in the function. In case of rational function, we first reduce expression by removing common factors from numerator and denominator.

Notification Switch
Would you like to follow the 'Functions' conversation and receive update notifications?