4.5 Geometric calculus of variations: vigre summer 2011  (Page 3/3)

which implies that:

$\square$

Also, this averaging will not affect the integral length of the function from side to side.

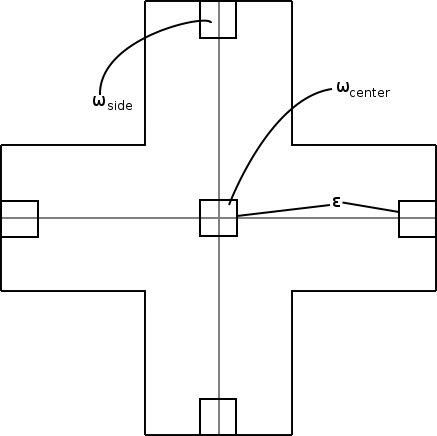
Another useful result is a bound on the metric at the center of the Swiss Cross.

Consider a discrete metric on the Swiss Cross. Then create a square in the center of the Swiss Cross with side length $ϵ$ , and other $ϵ$ squares at the center of the boundary of each outer square. If the weight in the center is $w_{center}$ , and the weight on the sides is $w_{side}$ then we want to minimize:

Diagram

subject to:

We can use Lagrange multipliers to solve this equation. So:

When we solve for the ratio $\frac{w_{center}}{w_{side}}$ , we get:

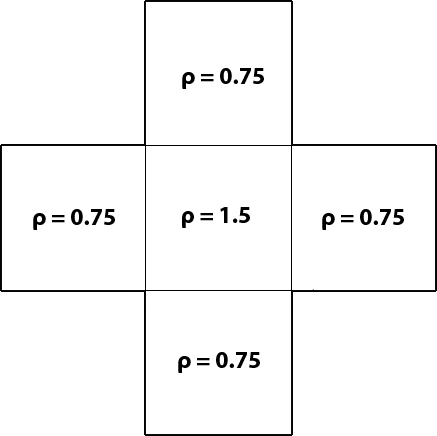
In order to find a lower bound for the metric area of the Swiss Cross, we can consider the simplified case where $\Gamma =\left\{\right(\text{Straight}\text{lines}\text{connecting}A\text{and}B)\cup (\text{Straight}\text{lines}\text{connecting}C\text{and}D\left)\right\}$ . It is easy to verify that the extremal metric is as shown in Figure 3. This function has a metric area of 4.5, so the minimum metric area for the entire set of curves $\Gamma$ will be greater than or equal to 4.5.

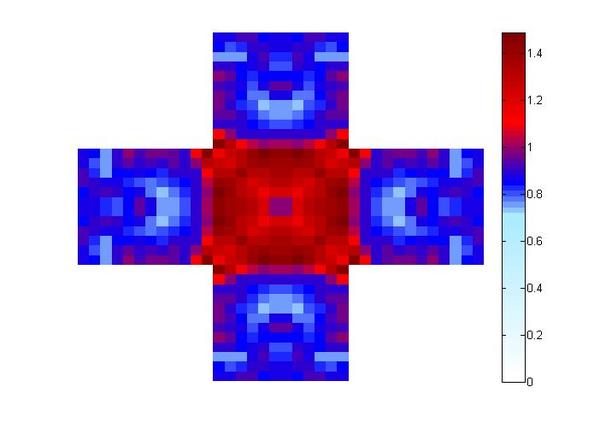
In order to visualize a solution, we used a recursive Matlab program to create an approximation of the extremal metric. Using a modified version of Dijkstra's algorithm we were able to find the shortest path between two sides, and progressively lower the metric area. In order to find a global minimum instead of a local, we used the method of gradient descent. Briefly, by selectively raising certain areas and rerunning the recursion, we wound up with a better metric area.

Diagram

Disk

Again, a prime candidate for extremal metric, $\rho \equiv 1$ seems reasonable which gives a metric area of $\pi$ . However, it is not extremal as is demonstrated in Figure 4. The metric area of Figure 4 is about 2.95, and it satisfies the constraints.

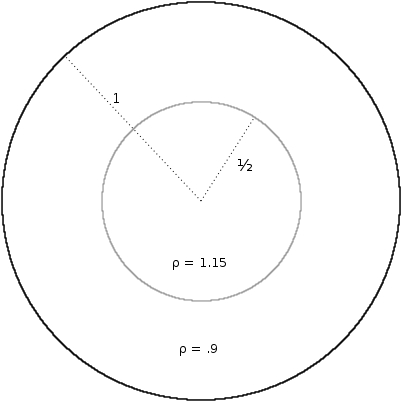
Using a symmetry argument similar to the Swiss Cross, it is evident that the metric on the disk will be a radial function, and hence in polar coordinates will have no $\theta$ dependence.

At this point it became useful to find a lower bound for the metric area of the circle. However, the straight line case is degenerate as every line passes through one point[1]. Thus using other methods it is possible to show that

Thus the extremal metric will have metric area between $\frac{8}{\pi }\approx$ 2.54 and 2.95.

Future work

A primary goal of any future work is creating a continuous minimizing metric on the disk and Swiss Cross. Further, some of the methods developed here can be applied to similar problems in extremal length. Many related problems involve sets of curves which connect two boundary sets. Specifically, the hexagon or Swiss hexagon (i.e. the hexagon with unit squares attached to the sides) are two interesting cases that could be the subject of further research.

Bibliography

1. Ahlfors, Lars V. Conformal Invariants: Topics in Geometric Function Theory . New York: McGraw-Hill, 1973. Print.

Acknowledgements

We would like to thank Mike Wolf, Colin Carroll, Leo Rosales, Bob Hardt, Paul Munger, and Renee Laverdiere for their help and guidance. We would also like to acknowledge the Rice University VIGRE program. A credit is due to the VIGRE program for the Summary section.