| << Chapter < Page | Chapter >> Page > |
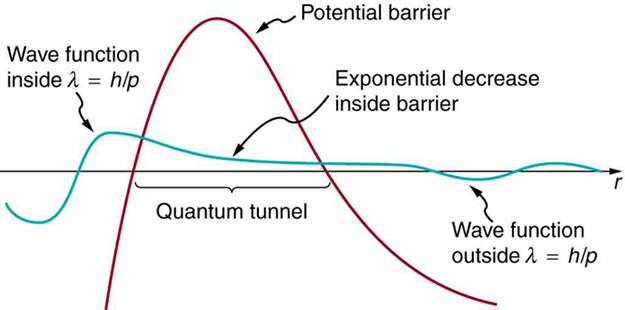
Good ideas explain more than one thing. In addition to qualitatively explaining how the four nucleons in an particle can get out of the nucleus, the detailed theory also explains quantitatively the half-life of various nuclei that undergo decay. This description is what Gamow and others devised, and it works for decay half-lives that vary by 17 orders of magnitude. Experiments have shown that the more energetic the decay of a particular nuclide is, the shorter is its half-life. Tunneling explains this in the following manner: For the decay to be more energetic, the nucleons must have more energy in the nucleus and should be able to ascend a little closer to the rim. The barrier is therefore not as thick for more energetic decay, and the exponential decrease of the wave function inside the barrier is not as great. Thus the probability of finding the particle outside the barrier is greater, and the half-life is shorter.
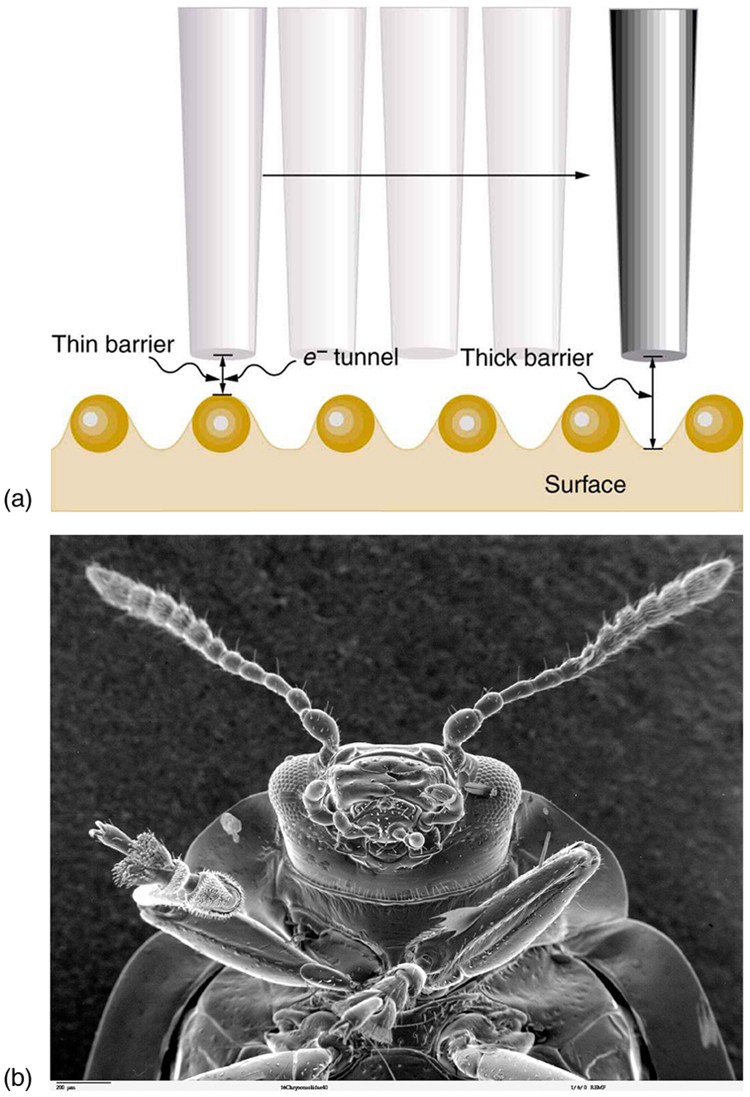
Tunneling as an effect also occurs in quantum mechanical systems other than nuclei. Electrons trapped in solids can tunnel from one object to another if the barrier between the objects is thin enough. The process is the same in principle as described for decay. It is far more likely for a thin barrier than a thick one. Scanning tunneling electron microscopes function on this principle. The current of electrons that travels between a probe and a sample tunnels through a barrier and is very sensitive to its thickness, allowing detection of individual atoms as shown in [link] .
Watch quantum "particles" tunnel through barriers. Explore the properties of the wave functions that describe these particles.

A physics student caught breaking conservation laws is imprisoned. She leans against the cell wall hoping to tunnel out quantum mechanically. Explain why her chances are negligible. (This is so in any classical situation.)
When a nucleus decays, does the particle move continuously from inside the nucleus to outside? That is, does it travel each point along an imaginary line from inside to out? Explain.
Derive an approximate relationship between the energy of decay and half-life using the following data. It may be useful to graph the log of against to find some straight-line relationship.
| Nuclide | ||
|---|---|---|
Integrated Concepts
A 2.00-T magnetic field is applied perpendicular to the path of charged particles in a bubble chamber. What is the radius of curvature of the path of a 10 MeV proton in this field? Neglect any slowing along its path.
22.8 cm
(a) Write the decay equation for the decay of . (b) What energy is released in this decay? The mass of the daughter nuclide is 231.036298 u. (c) Assuming the residual nucleus is formed in its ground state, how much energy goes to the particle?
(a)
(b) 4.679 MeV
(c) 4.599 MeV
Unreasonable Results
The relatively scarce naturally occurring calcium isotope has a half-life of about . (a) A small sample of this isotope is labeled as having an activity of 1.0 Ci. What is the mass of the in the sample? (b) What is unreasonable about this result? (c) What assumption is responsible?
Unreasonable Results
A physicist scatters rays from a substance and sees evidence of a nucleus in radius. (a) Find the atomic mass of such a nucleus. (b) What is unreasonable about this result? (c) What is unreasonable about the assumption?
a) u
(b) The greatest known atomic masses are about 260. This result found in (a) is extremely large.
(c) The assumed radius is much too large to be reasonable.
Unreasonable Results
A frazzled theoretical physicist reckons that all conservation laws are obeyed in the decay of a proton into a neutron, positron, and neutrino (as in decay of a nucleus) and sends a paper to a journal to announce the reaction as a possible end of the universe due to the spontaneous decay of protons. (a) What energy is released in this decay? (b) What is unreasonable about this result? (c) What assumption is responsible?
(a)
(b) Negative energy implies energy input is necessary and the reaction cannot be spontaneous.
(c) Although all conversation laws are obeyed, energy must be supplied, so the assumption of spontaneous decay is incorrect.
Construct Your Own Problem
Consider the decay of radioactive substances in the Earth’s interior. The energy emitted is converted to thermal energy that reaches the earth’s surface and is radiated away into cold dark space. Construct a problem in which you estimate the activity in a cubic meter of earth rock? And then calculate the power generated. Calculate how much power must cross each square meter of the Earth’s surface if the power is dissipated at the same rate as it is generated. Among the things to consider are the activity per cubic meter, the energy per decay, and the size of the Earth.

Notification Switch
Would you like to follow the 'College physics -- hlca 1104' conversation and receive update notifications?