| << Chapter < Page | Chapter >> Page > |
In this section, a design procedure is developed that uses a Chebyshev error criterion in both the passband and the stopband.This is the fourth possible combination of Chebyshev and Taylor's series approximations in the passband and stopband. The resultingfilter is called an elliptic-function filter, because elliptic functions are normally used to calculate the pole and zerolocations. It is also sometimes called a Cauer filter or a rational Chebyshev filter, and it has equal ripple approximation error inboth pass and stopbands [link] , [link] , [link] , [link] .
The error criteria of the elliptic-function filter are particularly well suited to the way specifications for filtersare often given. For that reason, use of the elliptic-function filter design usually gives the lowest order filter of the fourclassical filter design methods for a given set of specifications. Unfortunately, the design of this filter is themost complicated of the four. However, because of the efficiency of this class of filters, it is worthwhile gaining someunderstanding of the mathematics behind the design procedure.
This section sketches an outline of the theory of elliptic- function filter design. The details and properties of the ellipticfunctions themselves should simply be accepted, and attention put on understanding the overall picture. A more complete development isavailable in [link] , [link] . Straightforward design of elliptic-function filters can be accomplished by skipping this section and going directly toProgram 8 in the appendix or by using Matlab. However, it is important to understand the basics of the underlying theory to use the packaged designprograms intelligently.
Because both the passband and stopband approximations are over the entire bands, a transition band between the two must bedefined. Using a normalized passband edge, the bands are defined by
This is illustrated in [link] .
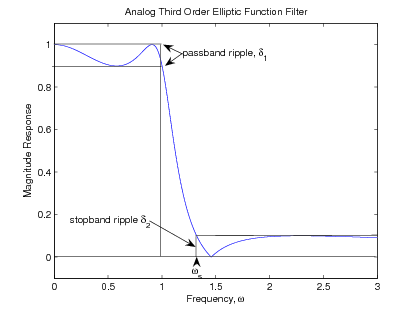
The characteristics of the elliptic function filter are best described in terms of the four parameters thatspecify the frequency response:
The result of the design is that for any three of the parameters given, the fourth is minimum. This is a very flexible andpowerful description of a filter frequency response.
The form of the frequency-response function is a generalization of that for the Chebyshev filter
where
with being the prototype analog filter transfer function similar to that for the Chebyshev filter. is a rational function that approximates zero in the passband and infinity inthe stopband. The definition of this function is a generalization of the definition of the Chebyshev polynomial.
In order to develop analytical expressions for equal-ripple rational functions, an interesting class of transcendentalfunctions, called the Jacobian elliptic functions, is outlined. These functions can be viewed as a generalization of the normaltrigonometric and hyperbolic functions. The elliptic integral of the first kind [link] is defined as

Notification Switch
Would you like to follow the 'Digital signal processing and digital filter design (draft)' conversation and receive update notifications?