| << Chapter < Page | Chapter >> Page > |
Find the unit normal vector for the vector-valued function and evaluate it at
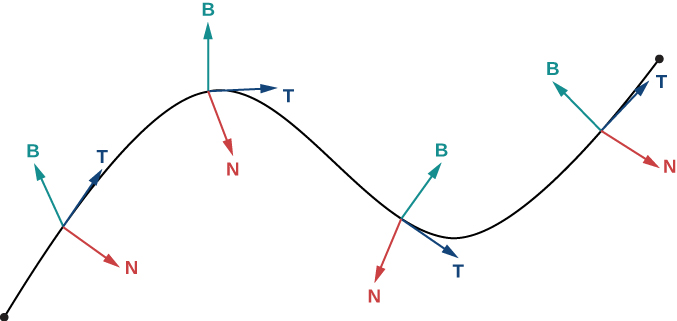
For any smooth curve in three dimensions that is defined by a vector-valued function, we now have formulas for the unit tangent vector T , the unit normal vector N , and the binormal vector B . The unit normal vector and the binormal vector form a plane that is perpendicular to the curve at any point on the curve, called the normal plane . In addition, these three vectors form a frame of reference in three-dimensional space called the Frenet frame of reference (also called the TNB frame) ( [link] ). Lat, the plane determined by the vectors T and N forms the osculating plane of C at any point P on the curve.
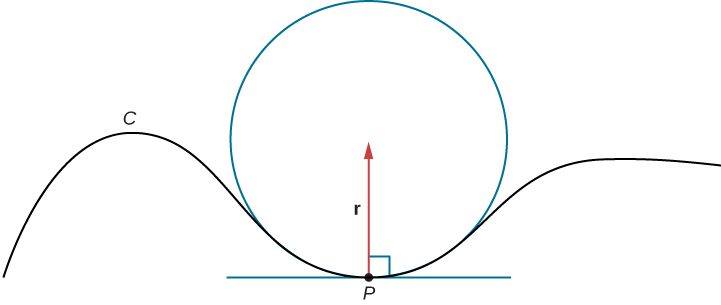
Suppose we form a circle in the osculating plane of C at point P on the curve. Assume that the circle has the same curvature as the curve does at point P and let the circle have radius r. Then, the curvature of the circle is given by We call r the radius of curvature of the curve, and it is equal to the reciprocal of the curvature. If this circle lies on the concave side of the curve and is tangent to the curve at point P, then this circle is called the osculating circle of C at P , as shown in the following figure.
For more information on osculating circles, see this demonstration on curvature and torsion, this article on osculating circles, and this discussion of Serret formulas.
To find the equation of an osculating circle in two dimensions, we need find only the center and radius of the circle.
Find the equation of the osculating circle of the helix defined by the function at
[link] shows the graph of
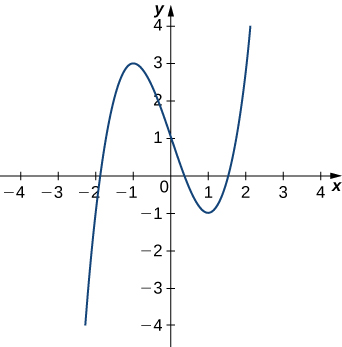
First, let’s calculate the curvature at
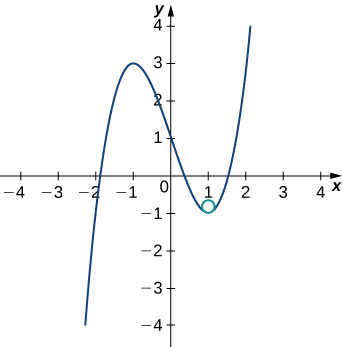
This gives Therefore, the radius of the osculating circle is given by Next, we then calculate the coordinates of the center of the circle. When the slope of the tangent line is zero. Therefore, the center of the osculating circle is directly above the point on the graph with coordinates The center is located at The formula for a circle with radius r and center is given by Therefore, the equation of the osculating circle is The graph and its osculating circle appears in the following graph.
Find the equation of the osculating circle of the curve defined by the vector-valued function at
At the point the curvature is equal to 4. Therefore, the radius of the osculating circle is
A graph of this function appears next:
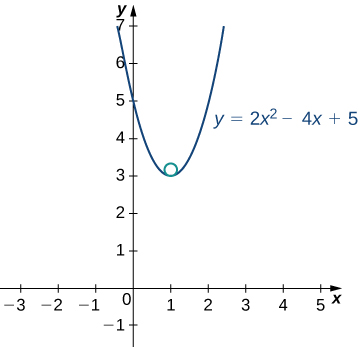
The vertex of this parabola is located at the point Furthermore, the center of the osculating circle is directly above the vertex. Therefore, the coordinates of the center are The equation of the osculating circle is

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?