| << Chapter < Page | Chapter >> Page > |
Бидејќи функција со две промеливи претставува површина во простор, таа може графички да се претстави во тродимензионален простор. Листот хартија на кој се претставува површина е дводимензионален, што тоа значи дека при графичкото претставување на функции со две променливи се намалува димензијата на просторот за еден, односно вршиме проекција на тродимензионалниот во дводимензионален простор. Пресметувањето на вредностите на функцијата за дадена точка не ни помага во графичкото претставување на функцијата, бидејки во просторот се добиваат бесконечно многу точки кои е тешко да се поврзат и од нив да се воочи обликот на површината. Затоа од помош се ниво-линиите кои го даваат обликот на кривата која се добива како пресек на површината со рамнини паралелни со координатните рамнини, или или .
Графички ќе ги прикажеме стандардните (елементарни) функции од две променливи. Тие се квадратните функции и од облик
.
Стандардните квадратни функции чии равенки се добиваат од наведената квадратна равенка се: сфера, елипсоид, параболоид, хиперболоид со едно или две крила, конус, хиперболичен параболоид, цилиндрични површини и рамнини. Рамнина се добива за , а рамнините беа подетално изучени во делот за Аналитичка геометрија во простор.
Сферата уште се нарекува и топка. Равенката на сфера со центар во точката
и радиус е
.
Специјално, сферата (Сл. 1) кога нејзиниот центар е во координатниот почеток е прикажана на Сл.1 и таа е со равенка
.
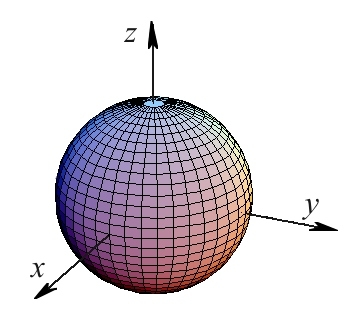 |
| Слика 1. Сфера со центар во координатниот почеток |
Кај сферата, сите пресеци со координатните рамнини се централни кружници со радиус , а пресеците со рамнини паралелни со координатните рамнини и на растојание помало од радиусот исто така се кружници.
Општата равенка на елипсоид со центар во точката и оски е
.
Специјален елипсоид (Сл. 2) е кога центарот е во координатниот почеток и има равенка
.
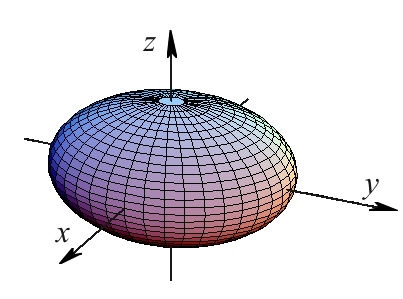 |
| Слика 2. Елипсоид со центар во координатниот почеток |
Кај елипсоидот, сите пресеци со координатните рамнини или рамнини паралелни со нив (на растојание помало од оските) се елипси.
Површината
е конусната површина или накусо конус (Сл. 3) со теме во координатниот почеток, издолжувањето е по оската, а пресеците со рамнини паралелни со рамнината се кружници. Пресеците со рамнини паралелни со координатните рамнини и се хиперболи.
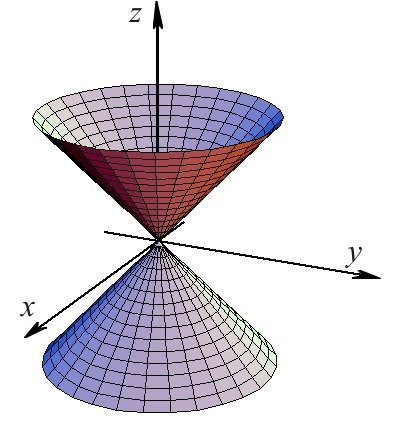 |
| Слика 3. Конус |
Поопшта равенка на конусна површина е елипсовидниот конус кај кого пресеците со рамнини паралелни со рамнината се елипси. Таквиот конус има равенка
.
Уште поопшта равенка на конусна површина е кога темето е во точката и тогаш конусот е со равенка
.
Еднокрилниот хиперболоид има равенка
,
и тоа е површина која е издолжена по оската (Сл. 4). Пресеците со рамнини паралелни со рамнината се кружници чии радиуси се поголеми од , а пресеците со рамнини паралелни со координатните рамнини и се хиперболи.
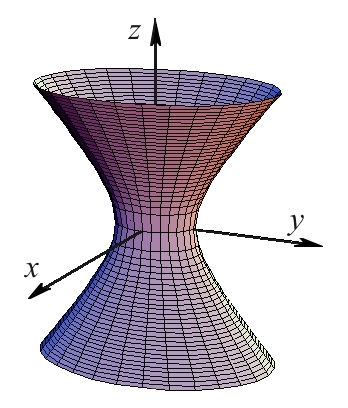 |
| Слика 4. Еднокрилен хиперболоид |
Кај елипсовидниот еднокрилен хиперболоид пресеците со рамнини паралелни со рамнината се елипси и тој има равенка
.
Површината со равенка
се нарекува двокрилен хиперболоид.
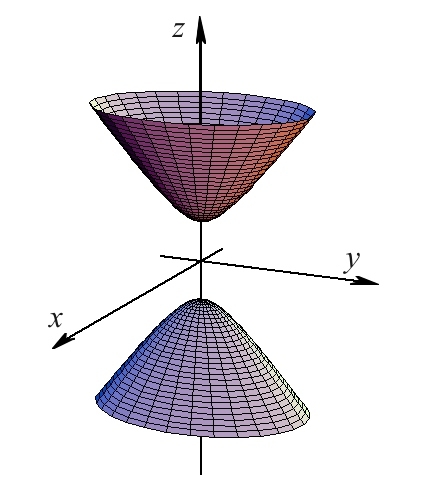 |
| Слика 5. Двокрилен хиперболоид |
Двете крила на хиперболоидот се распространети вдолж оската и има темиња во . Пресеците со рамнини паралелни со рамнината се кружници, а пресеците со рамнини паралелни со координатните рамнини и се хиперболи (Сл. 5). Двокрилниот хиперболоид исто така може да биде и елипсовиден и тој е со равенка
.
Параболоидот е површина која е зададена со равенката
Неговата равенка е квадратана функција по две променливи а по третата е линерна. За параболоидот е површина за која и се наоѓа во првите четири октанти. Темето е во координатниот почеток, пресеците со рамнини паралелни со рамнината се кружници, а пресеците со рамнини паралелни со координатните и рамнини се параболи (Сл.6).
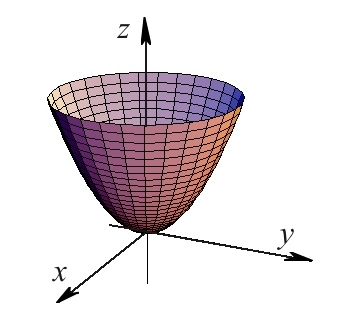 |
| Слика 6. Параболоид |
За параболоидот со отворот е свртен надолу. Поошт вид е елипсовидниот параболоид чии пресеци со рамнини паралелни со рамнината се елипси и има равенка
.
Хиперболичниот параболоид има равенка
.
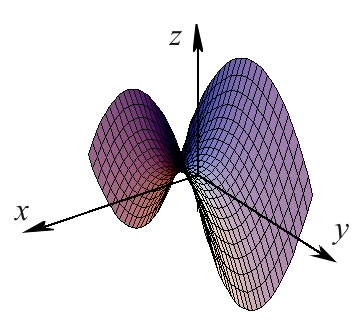 |
| Слика 7. Хиперболичен параболоид |
Тоа е површина чии пресеци со рамнини паралелни со рамнината се хиперболи, а пресеците со рамнини паралелни со координатните и рамнини се параболи (Сл. 7). Поопшт облик на хиперболичен параболоид се задава со равенката
.
Површини во простор во чија равенка се јавуваат само две променливи се нарекува цилиндрична површина. Најкарактеристична цилиндрична површина е цилиндерот.
Равенката
претставува цилиндер во простор чија основа е централна кружница во рамнината и изводниците од секоја точка од кружницата се паралелни со оската (Сл. 8).
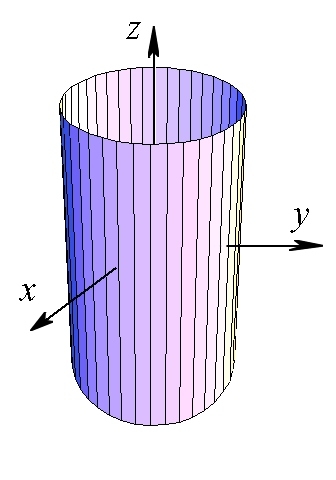 |
| Слика 8. Цилиндер |

Notification Switch
Would you like to follow the 'Математика 2' conversation and receive update notifications?